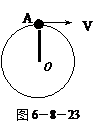
题目内容
如图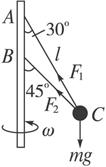
图
解析:由题意可看出,当小球角速度很小时,小球离心趋势小,只有绳AC拉紧,当小球角速度很大时,小球离心趋势大,只有绳BC拉紧,此两种情况小球所需向心力.
由两绳拉力分别与重力的合力提供,据牛顿第二定律与圆周运动知识可求得角速度的最小值与最大值,从而确定两绳同时拉紧的角速度范围.当ω=3 rad/s时,首先判断是那根绳子拉紧或者是同时拉紧,进而判断向心力来源,据牛顿第二定律与圆周运动知识列方程求得两绳拉力.
两绳张紧时,小球受重力mg,AC绳拉力F1和BC绳拉力F2如图所示.当角速度由0逐渐增大时,会出现两种临界情况.

(1)BC绳恰好拉直,F2=0,此时角速度为ω1,F1和mg的合力提供小球在半径r1=lsin30°的圆周上运动所需向心力,mgtan30°=mrω12,联立以上两式且代入数据得ω1=2.4 rad/s
AC绳仍拉直,但F1=0,此时角速度为ω2,F2和mg的合力提供向心力,mgtan45°=mr2ω2,r2=r1=lsin30°,联立解得ω2=3.2 rad/s,要两绳始终张紧,角速度的取值范围为2.4 rad/s≤ω≤3.2 rad/s.
(2)当ω=3 rad/s时,F1和F2同时存在,对小球应用牛顿第二定律有:
F1sin30°+F2sin45°=mlsin30°ω2,F1cos30°+F2cos45°-mg=0,两式联立且代入数据解得F1=0.27 N,F2=1.1 N.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目