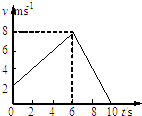��Ŀ����
����Ŀ����ͼ��ʾ��һ����m=0.4kg��С��飬��v0=2m/s�ij��ٶȣ�����б���ijһ�нǵ�����F�����£���б���������ȼ����˶�����t=2s��ʱ�������A���˶���B�㣬A��B֮��ľ���L=10m����֪б����Ǧ�=30o �� �����б��֮��Ķ�Ħ��������= ![]() ���������ٶ�gȡ10m/s2 ��
���������ٶ�gȡ10m/s2 �� 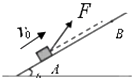
��1���������ٶȵĴ�С������B��ʱ�ٶȵĴ�С��
��2����������б��ļн�Ϊ30oʱ������F�Ĵ�С�Ƕ��٣�
���𰸡�
��1���⣺�������ٶȵĴ�СΪa������B��ʱ�ٶȵĴ�СΪv��
���˶�ѧ��ʽ�ã�L=v0t+ ![]() at2����
at2����
v=v0+at����
�����٢�ʽ���������ݽ�ã�
a=3m/s2����
v=8m/s����
�������ٶȵĴ�СΪ3m/s2������B��ʱ�ٶȵĴ�СΪ8m/s
��2���⣺���������֧����ΪFN������Ħ����ΪFf��
������б��֮��ļн�Ϊ��������������ͼ��ʾ��
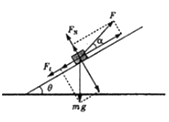
��ţ�ٵڶ����ɵã�
Fcos����mgsin�ȩ�Ff=ma����
Fsin��+FN��mgcos��=0����
��Ff=��FN�� ��
������ã�F= ![]() ����
����
�������ݵ�F��ֵΪ��Fmin= ![]() N
N
����������ͼ��ͼ��ʾ������F�Ĵ�СΪ ![]() N
N
����������1���������ȼ���ֱ���˶��������˶�ѧ��ʽ�����ٶȺ�ĩ�ٶȣ���2����������������������ţ�ٵڶ�������ʽ��������F�ı���ʽ�����������

 �����Ļ���������人������ϵ�д�
�����Ļ���������人������ϵ�д� ���������ּ���ÿһ��ȫ�º�����ҵ��ϵ�д�
���������ּ���ÿһ��ȫ�º�����ҵ��ϵ�д� ��ٽ������½������������ϵ�д�
��ٽ������½������������ϵ�д�