题目内容
7.在边长立为a的正方形的每个顶点都放置一个电荷量为q的点电荷.如果保持它们的位置不变,每个电荷受其他电荷的静电力是$\frac{{k{q^2}}}{a^2}$与$\frac{{k{q^2}}}{{2{a^2}}}$,其所受的合力是$\frac{{(2\sqrt{2}+1)k{q^2}}}{{2{a^2}}}$.分析 根据力的独立性原理和库仑定律,分别计算出其它三个电荷给它的库仑斥力大小,判断出方向,再根据力的合成法则,求出这三个力的合力即可.
解答 解:如图,假设第四个电荷q放在d点,则对角线上b点的电荷给它的库仑斥力为F1=k$\frac{{q}^{2}}{(\sqrt{2}a)^{2}}$=$\frac{{k{q^2}}}{{2{a^2}}}$,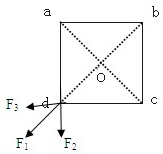 a电荷和c点的电荷给它的库仑斥力大小均为F2=F3=k$\frac{{q}^{2}}{{a}^{2}}$
a电荷和c点的电荷给它的库仑斥力大小均为F2=F3=k$\frac{{q}^{2}}{{a}^{2}}$
根据力的合成法则,点电荷q所受的电场力大小为:
F=k$\frac{{q}^{2}}{(\sqrt{2}a)^{2}}$+k$\frac{{q}^{2}}{{a}^{2}}$cos45°=$\frac{{(2\sqrt{2}+1)k{q^2}}}{{2{a^2}}}$;
故答案为:$\frac{{k{q^2}}}{a^2}$与$\frac{{k{q^2}}}{{2{a^2}}}$,$\frac{{(2\sqrt{2}+1)k{q^2}}}{{2{a^2}}}$.
点评 本题要知道库仑定律F=k$\frac{Qq}{{r}^{2}}$,以及力的独立性原理和求合力的方法,计算过程中要注意各个力的方向.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
15. 如图所示,一小球在光滑的V形槽中,由A点释放经B点到达与A点等高的C点.设A点的高度为1m,则下列说法中正确的是( )
如图所示,一小球在光滑的V形槽中,由A点释放经B点到达与A点等高的C点.设A点的高度为1m,则下列说法中正确的是( )
 如图所示,一小球在光滑的V形槽中,由A点释放经B点到达与A点等高的C点.设A点的高度为1m,则下列说法中正确的是( )
如图所示,一小球在光滑的V形槽中,由A点释放经B点到达与A点等高的C点.设A点的高度为1m,则下列说法中正确的是( )| A. | 在全过程中小球通过的位移和路程分别为1m和$\frac{4}{3}$$\sqrt{3}$m | |
| B. | 在由A到B的过程中,小球通过的位移和路程分别为$\frac{2}{3}$$\sqrt{3}$m和$\frac{2}{3}$$\sqrt{3}$m | |
| C. | 在全过程中,小球通过的位移和路程分别为$\frac{2}{3}$$\sqrt{3}$ m和$\frac{4}{3}$$\sqrt{3}$m | |
| D. | 在由A到C的过程中,小球通过的位移和路程分别为1m、1m |
2.关于电容器及其电容的叙述,正确的是( )
| A. | 任何两个彼此绝缘而又相互靠近的导体,就组成了电容器,跟这两个导体是否带电无关 | |
| B. | 电容器所带的电荷量是指每个极板所带电荷量的代数和 | |
| C. | 电容器的电容与电容器所带电荷量成反比 | |
| D. | 一个电容器的电荷量增加△Q=1.0×10-6 C时,两板间电压升高10 V,则电容器的电容变大了 |
12. 物体从斜面底部以一定的速率沿斜面向上运动,斜面底边水平,倾角可在0°~90°之间变化,物体沿斜面到达的最远距离x和倾角θ的关系如图所示,下列说法正确的是( )
物体从斜面底部以一定的速率沿斜面向上运动,斜面底边水平,倾角可在0°~90°之间变化,物体沿斜面到达的最远距离x和倾角θ的关系如图所示,下列说法正确的是( )
 物体从斜面底部以一定的速率沿斜面向上运动,斜面底边水平,倾角可在0°~90°之间变化,物体沿斜面到达的最远距离x和倾角θ的关系如图所示,下列说法正确的是( )
物体从斜面底部以一定的速率沿斜面向上运动,斜面底边水平,倾角可在0°~90°之间变化,物体沿斜面到达的最远距离x和倾角θ的关系如图所示,下列说法正确的是( )| A. | 物体与斜面间的动摩擦因数为μ=$\frac{{\sqrt{3}}}{3}$ | B. | 物体与斜面间的动摩擦因数为μ=$\frac{{\sqrt{3}}}{2}$ | ||
| C. | 当θ=30°时,x有最小值xmin=5$\sqrt{3}$m | D. | 当θ=60°时,x有最小值xmin=5$\sqrt{3}$m |
19.关于功的概念,下述说法中正确的是( )
| A. | 力越大,位移越大,做功就一定越多 | |
| B. | 力对物体做功越少,说明物体受的力越小 | |
| C. | 力很大,位移也很大,但这个力做的功可能为零 | |
| D. | 力对物体不做功,说明物体一定没有发生位移 |
16.某同学设计了一个探究加速度a与物体所受合力F及质量m关系的实验,图(a)为实验装置简图.(交流电的频率为50Hz)

(1)该实验要采用控制变量法法来进行研究;
(2)对于本实验,以下说法中正确的是DE
A.砂和桶的总质量m要远大于小车的总质量M
B.每次改变小车质量后,需要重新平衡摩擦力
C.小车的加速度可用a=$\frac{mg}{M}$求解
D.实验中也可不测加速度的具体数值,只要测出不同情况下加速度的比值就行了
E.若要验证“加速度与力的平方成正比”这一猜想,在作图线时最好以F2为横坐标
(3)图(b)为某次实验得到的纸带,根据纸带可求出小车的加速度大小为3.2m/s2.(保留二位有效数字)
(4)保持砂和砂桶质量不变,改变小车质量m,分别得到小车加速度a与质量m及对应的$\frac{1}{m}$,数据如表:
根据上表数据,为直观反映F不变时a与m的关系,请在图(d)方格坐标纸中选择恰当物理量建立坐标系,并作出图线.
(5)保持小车质量不变,改变砂和砂桶质量,该同学根据实验数据作出了加速度a随合力F的变化图线如图(c)所示.该图线不通过原点,其主要原因是物体受的摩擦力没有得到平衡或平衡摩擦力不足..

(1)该实验要采用控制变量法法来进行研究;
(2)对于本实验,以下说法中正确的是DE
A.砂和桶的总质量m要远大于小车的总质量M
B.每次改变小车质量后,需要重新平衡摩擦力
C.小车的加速度可用a=$\frac{mg}{M}$求解
D.实验中也可不测加速度的具体数值,只要测出不同情况下加速度的比值就行了
E.若要验证“加速度与力的平方成正比”这一猜想,在作图线时最好以F2为横坐标
(3)图(b)为某次实验得到的纸带,根据纸带可求出小车的加速度大小为3.2m/s2.(保留二位有效数字)
(4)保持砂和砂桶质量不变,改变小车质量m,分别得到小车加速度a与质量m及对应的$\frac{1}{m}$,数据如表:
| 实验次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 小车加速度a/m•s-2 | 1.90 | 1.72 | 1.49 | 1.25 | 1.00 | 0.75 | 0.50 | 0.30 |
| 小车质量m/kg | 0.25 | 0.29 | 0.33 | 0.40 | 0.50 | 0.71 | 1.00 | 1.67 |
| $\frac{1}{m}$/kg-1 | 4.00 | 3.45 | 3.03 | 2.50 | 2.00 | 1.41 | 1.00 | 0.60 |
(5)保持小车质量不变,改变砂和砂桶质量,该同学根据实验数据作出了加速度a随合力F的变化图线如图(c)所示.该图线不通过原点,其主要原因是物体受的摩擦力没有得到平衡或平衡摩擦力不足..
 如图所示,用绳子AC和BC悬一重力为100N的物体,绳子AC和BC与天花板的夹角分别为30°和60°,求每条绳子的拉力分别是多少?
如图所示,用绳子AC和BC悬一重力为100N的物体,绳子AC和BC与天花板的夹角分别为30°和60°,求每条绳子的拉力分别是多少?