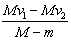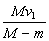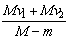题目内容
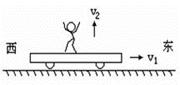
水平台球桌面上母球A、目标球B和球袋洞口边缘C位于一条直线上,设A、B两球质量均为0.25kg且可视为质点,A、B间的距离为5cm,B、C间距离为x=160cm,因两球相距很近,为避免“推杆”犯规(球杆推着两球一起运动的现象),常采用“点杆”击球法(当球杆杆头接触母球的瞬间,迅速将杆抽回,母球在离杆后与目标球发生对心正碰,因碰撞时间极短,可视为完全弹性碰撞),设球与桌面的动摩擦因数为μ=0.5,为使目标球可能落入袋中,求: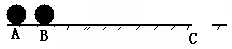
①碰撞过程中A球对B球的最小冲量为多大(碰撞过程中的摩擦阻力可忽略不计)
②碰撞前瞬间A球的速度最小是多大
1kg·m/s 4m/s
解析试题分析:Com]①设碰撞后瞬间B球能进入球袋的最小速度为vB,由动能定理得:
μmgx=0-=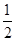 mvB2 解得vB="4m/s" (2分)
mvB2 解得vB="4m/s" (2分)
由动量定理得:I=mvB=1kg·m/s (2分)
②设A碰撞前瞬间最小速度为vA,碰撞后瞬间为v,则:
由动量守恒定律得:mvA=mv+mvB (2分)
由机械能守恒得: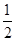 mvA2=
mvA2=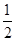 mv2+
mv2+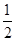 mvB2 (2分)
mvB2 (2分)
联立方程解得:vA=vB=4m/s,v=0 (1分)
考点:本题考查动量守恒定律。

 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案下面关于冲量的说法中正确的是( )
| A.物体受到很大的冲力时,其冲量一定很大 |
| B.当力与位移垂直时,该力的冲量为零 |
| C.不管物体做什么运动,在相同时间内重力的冲量相同 |
| D.只要力的大小恒定,其相同时间内的冲量就恒定 |
质量相等的甲乙两球在光滑水平面上沿同一直线运动。甲以7 kg·m/s的动量追上前方以5 kg·m/s的动量同向运动的乙球发生正碰,则碰后甲乙两球动量不可能的是
| A.6.5 kg·m/s, 5.5 kg·m/s | B.6 kg·m/s, 6 kg·m/s |
| C.4 kg·m/s, 8 kg·m/s | D.5.5 kg·m/s, 6.5 kg·m/s |
右端带有1/4光滑圆弧轨道质量为M的小车静置于光滑水平面上,如图所示.一质量为m的小球以速度v0水平冲上小车,关于小球此后的运动情况,以下说法正确的是( )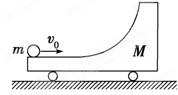
| A.小球可能从圆弧轨道上端抛出而不再回到小车 |
| B.小球不可能离开小车水平向左做平抛运动 |
| C.小球不可能离开小车做自由落体运动 |
| D.小球可能离开小车水平向右做平抛运动 |
如图所示,小车与木箱紧挨着静放在光滑的水平冰面上,现有一男孩站在小车上用力向右迅速推出木箱,关于上述过程,下列说法中正确的是 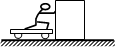
| A.男孩和木箱组成的系统动量守恒 |
| B.小车与木箱组成的系统动量守恒 |
| C.男孩、小车与木箱三者组成的系统动量守恒 |
| D.木箱的动量增量与男孩、小车的总动量增量相同 |
右图是“牛顿摆”装置,5个完全相同的小钢球用轻绳悬挂在水平支架上,5根轻绳互相平行,5个钢球彼此紧密排列,球心等高。用1、2、3、4、5分别标记5个小钢球。当把小球1向左拉起一定高度,如图甲所示,然后由静止释放,在极短时间内经过小球间的相互碰撞,可观察到球5向右摆起,且达到的最大高度与球1的释放高度相同,如图乙所示。关于此实验,下列说法中正确的是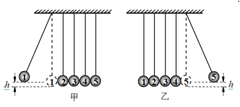
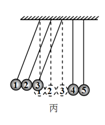
| A.上述实验过程中,5个小球组成的系统机械能守恒,动量守恒 |
| B.上述实验过程中,5个小球组成的系统机械能不守恒,动量不守恒 |
| C.如果同时向左拉起小球1、2、3到相同高度(如图丙所示),同时由静止释放,经碰撞后,小球4、5一起向右摆起,且上升的最大高度高于小球1、2、3的释放高度 |
| D.如果同时向左拉起小球1、2、3到相同高度(如图丙所示),同时由静止释放,经碰撞后,小球3、4、5一起向右摆起,且上升的最大高度与小球1、2、3的释放高度相同 |
一颗手榴弹以v0=10m/s的水平速度在空中飞行。设它爆炸后炸裂为两块,小块质量为0.2 kg,沿原方向以250 m/s的速度飞去,那么,质量为0.4 kg的大块在爆炸后速度大小和方向是
| A.125 m/s,与v0反向 |
| B.110 m/s,与v0反向 |
| C.240 m/s,与v0反向 |
| D.以上答案均不正确 |