Question

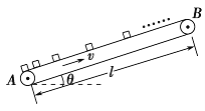
【题目】如图所示，与水平面成θ＝30°的传送带正以v＝3 m/s的速度匀速运行，A、B两端相距l＝13.5 m。现每隔1 s把质量m＝1 kg的工件(视为质点)轻放在传送带上，工件在传送带的带动下向上运动，工件与传送带间的动摩擦因数μ＝，取g＝10 m/s2，结果保留两位有效数字。求：

(1)相邻工件间的最小距离和最大距离；

(2)满载与空载相比，传送带需要增加多大的牵引力？

Answer 1

【答案】(1)0.50 m　3.0 m　(2)33 N

【解析】

（1）设工件在传送带上加速运动时的加速度为a，则由牛顿第二定律有：

代入数据可得加速度为：

刚放上下一个工件时，该工件离前一个工件的距离最小，且最小距离为：

当工件匀速运动时两相邻工件相距最远，则有：

（2）由于工件加速时间为，因此传送带上总有三个（n1=3)工件正在加速，故所有做 加速运动的工件对传送带的总滑动摩擦力：

在滑动摩擦力作用下工件移动的距离为：

所以传送带上匀速运动的工件个数为：

当工件与传送带相对静止后，每个工件受到的静摩擦力所以做匀速运动的工件对传送带的总静摩擦力

与空载相比，传送带需要增加的牵引力为：