题目内容
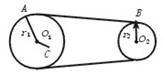
 如图所示,两轮靠皮带传动(不打滑),绷紧的皮带始终保持 v=3m/s的速度水平地匀速运动.一质量为m=1kg的小物体无初速地放到皮带轮的A处,若物体与皮带的动摩擦因数μ=0.2,AB间距离为L=5.25m.g取10m/s2.
如图所示,两轮靠皮带传动(不打滑),绷紧的皮带始终保持 v=3m/s的速度水平地匀速运动.一质量为m=1kg的小物体无初速地放到皮带轮的A处,若物体与皮带的动摩擦因数μ=0.2,AB间距离为L=5.25m.g取10m/s2.(1)求物体从A到B所需时间?
(2)物体从A到B的过程中因摩擦而转化的内能为多少?
(3)要使物体经B点后水平抛出,则皮带轮半径R不能超过多大?
分析:先判断物体从左端运动到右端做什么运动,然后根据运动学公式求解.
根据能量守恒定律,消耗的电能等于摩擦产生的内能与物体动能增量之和,摩擦产生的内能Wf=f△s.
从B点抛出后做平抛运动,则v<
.
根据能量守恒定律,消耗的电能等于摩擦产生的内能与物体动能增量之和,摩擦产生的内能Wf=f△s.
从B点抛出后做平抛运动,则v<
| gR |
解答:解:(1)物体无初速放到皮带上,受到皮带的摩擦力作用向右作初速为零的匀加速直线运动,有:a=
=
=
=μg=0.2×10m/s2=2m/s2
匀加速运动的时间为:t1=
=
s=1.5s
匀加速运动的位移为:s1=
=
m=2.25m
物体从1.5 s末开始以3 m/s的速度作匀速直线运动,有:
t2=
=
s=1s
故t=t1+t2=1.5s+1s=2.5s
(2)△E内=Q=Ffs相对=μmg(vt1-s1)=0.2×1×10(3×1.5-2.25)J=4.5J
(3)小物体达到B点时速度为3 m/s,皮带对小物体的支持力FN=0时R为最大,小物体仅受重力作用从B点水平抛出,有:mg=m
R=
=
m=0.9m
答:(1)求物体从A到B所需时间为1.5s.
(2)物体从A到B的过程中因摩擦而转化的内能为4.5J.
(3)要使物体经B点后水平抛出,则皮带轮半径R不能超过0.9m.
| Ff |
| m |
| μFN |
| m |
| μmg |
| m |
匀加速运动的时间为:t1=
| v |
| a |
| 3 |
| 2 |
匀加速运动的位移为:s1=
| v2 |
| 2a |
| 32 |
| 2×2 |
物体从1.5 s末开始以3 m/s的速度作匀速直线运动,有:
t2=
| L-s1 |
| v |
| 5.25-2.25 |
| 3 |
故t=t1+t2=1.5s+1s=2.5s
(2)△E内=Q=Ffs相对=μmg(vt1-s1)=0.2×1×10(3×1.5-2.25)J=4.5J
(3)小物体达到B点时速度为3 m/s,皮带对小物体的支持力FN=0时R为最大,小物体仅受重力作用从B点水平抛出,有:mg=m
| v2 |
| R |
R=
| v2 |
| g |
| 32 |
| 10 |
答:(1)求物体从A到B所需时间为1.5s.
(2)物体从A到B的过程中因摩擦而转化的内能为4.5J.
(3)要使物体经B点后水平抛出,则皮带轮半径R不能超过0.9m.
点评:解决本题的关键会根据受力判断物体的运动情况,以及知道消耗的电能等于摩擦产生的内能与物体动能增量之和.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案
相关题目
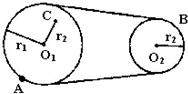 如图所示的两轮靠皮带传动,皮带没有打滑,A、B、C三点的位置关系如图,若r1>r2,O1C=r2,则三点的向心加速度的关系为( )
如图所示的两轮靠皮带传动,皮带没有打滑,A、B、C三点的位置关系如图,若r1>r2,O1C=r2,则三点的向心加速度的关系为( )