题目内容
19.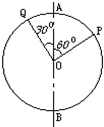 一圆环,其圆心为O,若以它的直径AB为轴做匀速转动,如图所示.则圆环上P、Q两点向心加速度之比( )
一圆环,其圆心为O,若以它的直径AB为轴做匀速转动,如图所示.则圆环上P、Q两点向心加速度之比( )| A. | 1:1 | B. | 1:2 | C. | 1:$\sqrt{3}$ | D. | $\sqrt{3}$:1 |
分析 同一圆环以直径为轴做匀速转动时,环上的点的角速度相同,根据几何关系可以求得Q、P两点各自做圆周运动的半径,根据a=ω2r即可求解向心加速度之比.
解答 解:P、Q两点以它的直径AB为轴做匀速转动,它们的角速度相同都为ω,
所以P点转动的半径:
r1=Rsin60°=$\frac{\sqrt{3}}{2}$R
Q点转动的半径:
r2=Rsin30°=$\frac{1}{2}$R
根据a=ω2r得:
$\frac{{a}_{P}}{{a}_{Q}}=\frac{{r}_{1}}{{r}_{2}}=\frac{\frac{\sqrt{3}}{2}R}{\frac{1}{2}R}=\sqrt{3}$
故选:D
点评 本题关键是明确同轴传动角速度相等,然后结合公式a=ω2r求解向心加速度之比,基础题目.

练习册系列答案
相关题目
10.根据下列数据,可以算出阿伏加德罗常数的是( )
| A. | 水的密度和水的摩尔质量 | B. | 水的摩尔质量和水分子的体积 | ||
| C. | 水的摩尔质量和水分子的质量 | D. | 水分子的体积和水分子的质量 |
14.质量不同的两个物体从同一高度静止释放后落到地面,不计空气阻力,下列说法中正确的是( )
| A. | 落地的时间不同 | B. | 落地时的速度不同 | ||
| C. | 它们的运动不是自由落体运动 | D. | 下落过程中物体的加速度相同 |
4.两个质量相等的物体,分别从两个高度相等而倾角不同的光滑斜面顶从静止开始下滑,则下列说法正确的是( )
| A. | 到达底部时重力的功率相等 | B. | 到达底部时速度相等 | ||
| C. | 下滑过程中重力做的功相等 | D. | 到达底部的时间相等 |
11.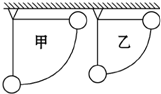 甲、乙两球的质量相等,悬线一长一短,将两球由图示位置的同一水平面无初速度释放,不计阻力,则对小球过最低点时的正确说法是( )
甲、乙两球的质量相等,悬线一长一短,将两球由图示位置的同一水平面无初速度释放,不计阻力,则对小球过最低点时的正确说法是( )
 甲、乙两球的质量相等,悬线一长一短,将两球由图示位置的同一水平面无初速度释放,不计阻力,则对小球过最低点时的正确说法是( )
甲、乙两球的质量相等,悬线一长一短,将两球由图示位置的同一水平面无初速度释放,不计阻力,则对小球过最低点时的正确说法是( )| A. | 甲球的动能与乙球的动能相等 | |
| B. | 两球受到线的拉力大小相等 | |
| C. | 两球的向心加速度大小相等 | |
| D. | 相对同一参考面,两球的机械能相等 |
8.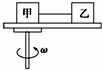 一圆盘可以绕其竖直轴在水平面内转动,圆盘半径为R,甲、乙两物体的质量分别为M与m(M>m),它们与圆盘之间的最大静摩擦力均为正压力的μ倍,两物体用一根长为l(l<R)的轻绳连在一起,如图,甲物体放在转动轴的位置上,甲、乙之间的连线刚好沿半径方向拉直,要使两物体与圆盘之间不发生相对滑动,则圆盘旋转的角速度最大值不得超过( )
一圆盘可以绕其竖直轴在水平面内转动,圆盘半径为R,甲、乙两物体的质量分别为M与m(M>m),它们与圆盘之间的最大静摩擦力均为正压力的μ倍,两物体用一根长为l(l<R)的轻绳连在一起,如图,甲物体放在转动轴的位置上,甲、乙之间的连线刚好沿半径方向拉直,要使两物体与圆盘之间不发生相对滑动,则圆盘旋转的角速度最大值不得超过( )
 一圆盘可以绕其竖直轴在水平面内转动,圆盘半径为R,甲、乙两物体的质量分别为M与m(M>m),它们与圆盘之间的最大静摩擦力均为正压力的μ倍,两物体用一根长为l(l<R)的轻绳连在一起,如图,甲物体放在转动轴的位置上,甲、乙之间的连线刚好沿半径方向拉直,要使两物体与圆盘之间不发生相对滑动,则圆盘旋转的角速度最大值不得超过( )
一圆盘可以绕其竖直轴在水平面内转动,圆盘半径为R,甲、乙两物体的质量分别为M与m(M>m),它们与圆盘之间的最大静摩擦力均为正压力的μ倍,两物体用一根长为l(l<R)的轻绳连在一起,如图,甲物体放在转动轴的位置上,甲、乙之间的连线刚好沿半径方向拉直,要使两物体与圆盘之间不发生相对滑动,则圆盘旋转的角速度最大值不得超过( )| A. | $\sqrt{\frac{μ(M-m)g}{ml}}$ | B. | $\sqrt{\frac{μ(M-m)g}{Ml}}$ | C. | $\sqrt{\frac{μ(M+m)g}{Ml}}$ | D. | $\sqrt{\frac{μ(M+m)g}{ml}}$ |
9.下列各过程中所指出的力,做功为零的有( )
| A. | 肩负重物的人沿水平路面行走时,肩对重物的支持力 | |
| B. | 汽车沿斜坡向上运动时,斜坡对汽车的支持力 | |
| C. | 用手指捏住玻璃板竖直提起时,手指对板的压力 | |
| D. | 放在水平传送带上的物体,随传送带以相同加速度运动时,物体对传送带的摩擦力 |
 如图所示,在光滑的水平面上有A、B两辆质量均为m的小车,保持静止状态,A车上站着一个质量为$\frac{m}{2}$的人,当人从A车跳到B车上,并与B车保持相对静止,则A车与B车速度大小比等于3:2.
如图所示,在光滑的水平面上有A、B两辆质量均为m的小车,保持静止状态,A车上站着一个质量为$\frac{m}{2}$的人,当人从A车跳到B车上,并与B车保持相对静止,则A车与B车速度大小比等于3:2.