Question

（2007?江苏）如图所示，巡查员站立于一空的贮液池边，检查池角处出液口的安全情况．已知池宽为L，照明灯到池底的距离为H．若保持照明光束方向不变，向贮液池中注入某种液体，当液面高为

H

2

时，池底的光斑距离出液口

L

4

．
（1）试求当液面高为

2

3

H时，池底的光斑到出液口的距离x．
（2）控制出液口缓慢地排出液体，使液面以v₀的速率匀速下降，试求池底的光斑移动的速率v_x．

Answer 1

分析：（1）当光从空气射向水中时，根据几何关系从而确定入射角的正弦值与折射角的正弦值，从而由光的折射定律可算出水的折射率．当液面高度改变时，即入射点发生变化，但入射角与折射角均没有变化，所以通过几何关系可以确定池底的光斑到出液口的距离．
（2）液面匀速下降时，光斑也在匀速向左运动．所以由位移与速度的比值相等可列式，从而求出光斑的运动速度．

解答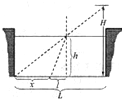：解：（1）由几何关系知：

x+l

h

=

L

H

由折射定律得：

L

L2+H2

=n?

l

l2+h2

代入h=

H

2

，l=

L

4

得：n=

L2+4H2

L2+H2

由于x=

L

2H

h
解得：x=

L

3

（2）液面匀速下降，光斑也匀速向左运动．
则有

L 4

vx

=

H 2

vH

，
整理得 vx=

L

2H

vh．

点评：虽然液面高度变化，但由于入射角没变，则折射角也不变．于是可以根据几何关系来构建长度关系，从而求出所求结果．当液面高度匀速变化时，光斑也匀速变化，因此利用同时性，来列出等式，从而确定光斑运动的速度．