题目内容
 如图所示为车站使用的水平传送带的模型,它的水平传送带的长度为l=8m,传送带的皮带轮的半径为r=0.2m,传送带的上部距地面的高度为h=0.45m,现有一个旅行包(视为质点)以v0=10m/s的初速度水平地滑上水平传送带.已知旅行包与皮带之间的动摩擦因数为μ=0.6,g=10m/s2.试讨论下列问题:
如图所示为车站使用的水平传送带的模型,它的水平传送带的长度为l=8m,传送带的皮带轮的半径为r=0.2m,传送带的上部距地面的高度为h=0.45m,现有一个旅行包(视为质点)以v0=10m/s的初速度水平地滑上水平传送带.已知旅行包与皮带之间的动摩擦因数为μ=0.6,g=10m/s2.试讨论下列问题:(1)若传送带静止,旅行包滑到B端时,人若没有及时取下,旅行包将从B端滑落,则包的落地点距B端的水平距离为多少?
(2)设皮带轮顺时针匀速转动,并设水平传送带长度仍为l=8m,旅行包滑上传送带的初速度恒为v0=10m/s.当皮带的角速度ω值在什么范围内,旅行包落地点距B端的水平距离始终为(1)中所求的距离?若皮带的角速度ω1=40rad/s,旅行包落地点距B端的水平距离又是多少?
分析:(1)旅行包向右滑动,受到重力、支持力和滑动摩擦力,根据牛顿第二定律列式求加速度,然后根据速度位移公式列式求解末速度,最后根据平抛运动的分位移公式求解水平射程;
(2)如果旅行包一直减速,到达最右端的速度与传送带不动时的速度相同,则平抛的初速度相同,射程也就相同,故只需传送带的速度小于旅行箱到达最右端的速度即可;皮带的角速度ω1=40rad/s,旅行箱先减速后匀速,根据运动学公式和平抛运动的分位移公式列式求解.
(2)如果旅行包一直减速,到达最右端的速度与传送带不动时的速度相同,则平抛的初速度相同,射程也就相同,故只需传送带的速度小于旅行箱到达最右端的速度即可;皮带的角速度ω1=40rad/s,旅行箱先减速后匀速,根据运动学公式和平抛运动的分位移公式列式求解.
解答:解:(1)若传送带静止,则旅行包滑上水平传送带后做匀减速运动,其加速度a=μg=6m/s2
旅行包到达B端的水平速度为v=
=2m/s
旅行包离开传送带后做平抛运动,落地点距B端的水平距离为
S=vt=v
=0.6m
即包的落地点距B端的水平距离为0.6m.
(2)若皮带轮顺时针匀速转动,要使旅行包落地点距B端的水平距离始终为(1)中所示的水平距离,则旅行包须做匀减速运动,皮带轮的临界角速度为
ω0=
=10rad/s
所以ω的取值范围是ω≤10rad/s;
当ω1=40rad/s时,皮带线速度v1=ω1r=8m/s
当旅行包速度也为v1=8m/s,在皮带上运动了S=
=3m<8m
以后旅行包做匀速直线运动.所以旅行包到达B端的速度也为8m/s.包的落地点距B端的水平距离S1=v1
=2.4m;
故当皮带的角速度ω值的取值范围是ω≤10rad/s时,旅行包落地点距B端的水平距离始终为(1)中所求的距离,若皮带的角速度ω1=40rad/s,旅行包落地点距B端的水平距离为2.4m.
旅行包到达B端的水平速度为v=
|
旅行包离开传送带后做平抛运动,落地点距B端的水平距离为
S=vt=v
|
即包的落地点距B端的水平距离为0.6m.
(2)若皮带轮顺时针匀速转动,要使旅行包落地点距B端的水平距离始终为(1)中所示的水平距离,则旅行包须做匀减速运动,皮带轮的临界角速度为
ω0=
| v |
| r |
所以ω的取值范围是ω≤10rad/s;
当ω1=40rad/s时,皮带线速度v1=ω1r=8m/s
当旅行包速度也为v1=8m/s,在皮带上运动了S=
| ||||
| 2a |
以后旅行包做匀速直线运动.所以旅行包到达B端的速度也为8m/s.包的落地点距B端的水平距离S1=v1
|
故当皮带的角速度ω值的取值范围是ω≤10rad/s时,旅行包落地点距B端的水平距离始终为(1)中所求的距离,若皮带的角速度ω1=40rad/s,旅行包落地点距B端的水平距离为2.4m.
点评:本题关键是对小滑块的运动情况分析清楚,然后根据牛顿第二定律、运动学公式和平抛运动的分位移公式列式求解.

练习册系列答案
相关题目
 如图所示为车站使用的水平传送带的模型,它的水平传送带的长度为L=8m,传送带的上部距地面的高度为h=0.45m,现有一个旅行包(视为质点)以速度v0=10m/s的初速度水平地滑上水平传送带.已知旅行包与皮带之间的动摩擦因数为μ=
如图所示为车站使用的水平传送带的模型,它的水平传送带的长度为L=8m,传送带的上部距地面的高度为h=0.45m,现有一个旅行包(视为质点)以速度v0=10m/s的初速度水平地滑上水平传送带.已知旅行包与皮带之间的动摩擦因数为μ= (2007?莱芜模拟)如图所示为车站使用的水平传送带的模型,它的水平传送带的长度为L=8m,A、B为传送带水平部分的最左端和最右端.现有一个旅行包(视为质点)以v0=10m/s的初速度从A端水平地滑上水平传送带.已知旅行包与传送带之间的动摩擦因数为μ=0.6.试求:
(2007?莱芜模拟)如图所示为车站使用的水平传送带的模型,它的水平传送带的长度为L=8m,A、B为传送带水平部分的最左端和最右端.现有一个旅行包(视为质点)以v0=10m/s的初速度从A端水平地滑上水平传送带.已知旅行包与传送带之间的动摩擦因数为μ=0.6.试求: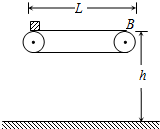 如图所示为车站使用的水平传送带的模型,它的水平传送带的长度为L=8m,传送带的皮带轮的半径均为R=0.2m,传送带的上部距地面的高度为h=0.45m,现有一个旅行包(视为质点)以速度v0=10m/s的初速度水平地滑上水平传送带.已知旅行包与皮带之间的动摩擦因数为μ=0.6.皮带轮与皮带之间始终不打滑,g取10m/s2.讨论下列问题:
如图所示为车站使用的水平传送带的模型,它的水平传送带的长度为L=8m,传送带的皮带轮的半径均为R=0.2m,传送带的上部距地面的高度为h=0.45m,现有一个旅行包(视为质点)以速度v0=10m/s的初速度水平地滑上水平传送带.已知旅行包与皮带之间的动摩擦因数为μ=0.6.皮带轮与皮带之间始终不打滑,g取10m/s2.讨论下列问题: 如图所示为车站使用的水平传送带装置的示意图,绷紧的传送带始终保持恒定速率运行,传送带的水平部分AB距离水平地面的高度h=0.45m.现有一行李包(可视为质点)由A端被传送到B端,且传送到B端时没有及时取下,行李包从B端水平抛出,不计空气阻力,g取10m/s2.
如图所示为车站使用的水平传送带装置的示意图,绷紧的传送带始终保持恒定速率运行,传送带的水平部分AB距离水平地面的高度h=0.45m.现有一行李包(可视为质点)由A端被传送到B端,且传送到B端时没有及时取下,行李包从B端水平抛出,不计空气阻力,g取10m/s2.