题目内容
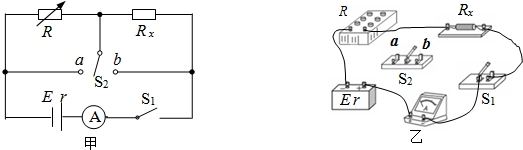
如图甲所示,放置在水平桌面上的两条不计电阻的光滑导轨间的距离L=1m,质量m=3kg,长为1m,电阻为r的光滑导体棒放在导轨上,导轨左端与阻值R=3Ω的电阻相连,导轨所在位置有磁感应强度为B=2T的足够大的匀强磁场,磁场的方向垂直导轨平面向下,现在给导体棒施加一个水平向右的拉力F,乙图是导体棒运动的v-t图象,其中OA、BC段是直线,AB段是曲线.假设在1s以后拉力的功率保持不变,3s后拉力F=10N,导体棒在运动过程中始终与导轨垂直,且接触良好.g取10m/s2,设导轨足够长,求:
(1)电阻r的大小.
(2)t=0.6s时,拉力F的大小.
(3)计算1s到3s的时间内电阻R上产生的热量.

(1)电阻r的大小.
(2)t=0.6s时,拉力F的大小.
(3)计算1s到3s的时间内电阻R上产生的热量.
分析:(1)由图象可知,3s后导体棒做匀速直线运动,处于平衡状态,由图象可以求出导体棒的速度,由E=BIL、欧姆定律、安培力公式可以求出导体棒受到的安培力,然后由平衡条件列方程求出电阻r的大小.
(2)由图象可知,在0~1s时间内,导体棒做匀加速直线运动,由图象求出导体棒的加速度,由速度公式求出t=0.6s时的速度,由安培力公式求导体棒受到的安培力,最后由牛顿第二定律求出此时的拉力.
(3)由P=Fv求出1~3s内拉力的功率,由能量守恒定律求出在此期间电阻R上产生的热量.
(2)由图象可知,在0~1s时间内,导体棒做匀加速直线运动,由图象求出导体棒的加速度,由速度公式求出t=0.6s时的速度,由安培力公式求导体棒受到的安培力,最后由牛顿第二定律求出此时的拉力.
(3)由P=Fv求出1~3s内拉力的功率,由能量守恒定律求出在此期间电阻R上产生的热量.
解答:解:(1)由图象可知,导体棒运动的速度达到10m/s时开始做匀速运动,
导体棒匀速运动的速度v=10m/s.
匀速运动后导体棒上的电动势:E=BLv,
导体棒受的安培力:F1=BIL=B
L=
,
导体棒做匀速直线运动,处于平衡状态,
由平衡条件得:F=
,
电阻r=
-R=
-3=1Ω;
(2)由图象可知,在0~1s内,导体棒做匀速直线运动,
加速度a=
=
=5m/s2,
在时间t=0.6s时导体棒的速度v′=at=5×0.6=3m/s.
此时导体棒受到的安培力:F2=BIL=
=
=3N,
对导体棒,由牛顿定律得:F-F2=ma,
拉力F=-F2+ma=3+3×5=18N;
(3)在1s~3s的t=2s内,F的功率恒定P=Fv=10×10=100W,
由图示可知,t1=1s时,v1=5m/s,t2=3s时,v2=10m/s,
由能量守恒定律得:Pt-Q=
mv22-
mv12,代入数据解得:Q=87.5J,
R上产生的热量QR=
=
=65.625J;
答:(1)电阻r的大小为1Ω.(2)t=0.6s时,拉力F的大小为18N.(3)计算1s到3s的时间内电阻R上产生的热量为65.625J.
导体棒匀速运动的速度v=10m/s.
匀速运动后导体棒上的电动势:E=BLv,
导体棒受的安培力:F1=BIL=B
| E |
| r+R |
| B2L2v |
| r+R |
导体棒做匀速直线运动,处于平衡状态,
由平衡条件得:F=
| B2L2v |
| r+R |
电阻r=
| B2L2 v |
| F |
| 22×1×10 |
| 10 |
(2)由图象可知,在0~1s内,导体棒做匀速直线运动,
加速度a=
| △v |
| △t |
| 5 |
| 1 |
在时间t=0.6s时导体棒的速度v′=at=5×0.6=3m/s.
此时导体棒受到的安培力:F2=BIL=
| B2L2v′ |
| r+R |
| 22×1×3 |
| 1+3 |
对导体棒,由牛顿定律得:F-F2=ma,
拉力F=-F2+ma=3+3×5=18N;
(3)在1s~3s的t=2s内,F的功率恒定P=Fv=10×10=100W,
由图示可知,t1=1s时,v1=5m/s,t2=3s时,v2=10m/s,
由能量守恒定律得:Pt-Q=
| 1 |
| 2 |
| 1 |
| 2 |
R上产生的热量QR=
| QR |
| r+R |
| 87.5×3 |
| 1+3 |
答:(1)电阻r的大小为1Ω.(2)t=0.6s时,拉力F的大小为18N.(3)计算1s到3s的时间内电阻R上产生的热量为65.625J.
点评:本题是一道力、电、磁综合题,考查了求电阻、力、热量等问题,分析清楚导体棒的运动过程、由图象求出导体棒的时间对应的速度、根据图象判断出导体棒的运动性质、应用相关公式即可正确解题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图甲所示,水平加速电场的加速电压为U0,在它的右侧有由水平正对放置的平行金属板a、b构成的偏转电场,已知偏转电场的板长L=0.10m,板间距离d=5.0×10-2 m,两板间接有如图15乙所示的随时间变化的电压U,且a板电势高于b板电势.在金属板右侧存在有界的匀强磁场,磁场的左边界为与金属板右侧重合的竖直平面MN,MN右侧的磁场范围足够大,磁感应强度B=5.0×10-3T,方向与偏转电场正交向里(垂直纸面向里).质量和电荷量都相同的带正电的粒子从静止开始经过电压U0=50V的加速电场后,连续沿两金属板间的中线OO′方向射入偏转电场中,中线OO′与磁场边界MN垂直.已知带电粒子的比荷
如图甲所示,水平加速电场的加速电压为U0,在它的右侧有由水平正对放置的平行金属板a、b构成的偏转电场,已知偏转电场的板长L=0.10m,板间距离d=5.0×10-2 m,两板间接有如图15乙所示的随时间变化的电压U,且a板电势高于b板电势.在金属板右侧存在有界的匀强磁场,磁场的左边界为与金属板右侧重合的竖直平面MN,MN右侧的磁场范围足够大,磁感应强度B=5.0×10-3T,方向与偏转电场正交向里(垂直纸面向里).质量和电荷量都相同的带正电的粒子从静止开始经过电压U0=50V的加速电场后,连续沿两金属板间的中线OO′方向射入偏转电场中,中线OO′与磁场边界MN垂直.已知带电粒子的比荷 (2011?罗湖区模拟)某校研究性学习小组的同学用如图甲所示的滴水法测量一小车在斜面上运动时的加速度.实验过程如下:在斜面上铺上白纸,用图钉钉住;把滴水计时器固定在小车的末端;调节滴水计时器的滴水速度,使其每0.2s滴一滴(以滴水计时器内盛满水为准);在斜面顶端放置一浅盘,把小车放在斜面顶端,把调好的滴水计时器盛满水,使水滴能滴人浅盘内;随即在撤去浅盘的同时放开小车,于是水滴在白纸上留下标志小车运动规律的点迹;小车到达斜面底端时立即将小车移开.
(2011?罗湖区模拟)某校研究性学习小组的同学用如图甲所示的滴水法测量一小车在斜面上运动时的加速度.实验过程如下:在斜面上铺上白纸,用图钉钉住;把滴水计时器固定在小车的末端;调节滴水计时器的滴水速度,使其每0.2s滴一滴(以滴水计时器内盛满水为准);在斜面顶端放置一浅盘,把小车放在斜面顶端,把调好的滴水计时器盛满水,使水滴能滴人浅盘内;随即在撤去浅盘的同时放开小车,于是水滴在白纸上留下标志小车运动规律的点迹;小车到达斜面底端时立即将小车移开.