题目内容
5.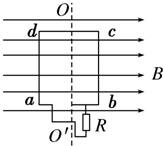 如图所示,矩形线圈abcd在磁感应强度B=2T的匀强磁场中绕轴OO′以角速度ω=10π rad/s匀角速转动,线圈共10匝,线圈总电阻r=5Ω,ab=0.3m,bc=0.6m,负载电阻R=45Ω.求:
如图所示,矩形线圈abcd在磁感应强度B=2T的匀强磁场中绕轴OO′以角速度ω=10π rad/s匀角速转动,线圈共10匝,线圈总电阻r=5Ω,ab=0.3m,bc=0.6m,负载电阻R=45Ω.求:(1)写出从图示位置开始计时线圈中感应电动势的瞬时值表达式;
(2)感应电流的有效值;
(3)从图示位置开始计时0.05s内平均感应电流的大小.
分析 (1)根据公式Em=nBsω求解感应电动势的最大值,再根据e=Emsinωt求解瞬时值表达式;
(2)由欧姆定律可求得电流,注意有效值与最大值的关系;
(3)根据角速度与周期的关系明确转动时间,再由法拉第电磁感应定律求得平均电流.
解答 解:(1)电动势的最大值为:
Em=nBSω=10×2×0.3×0.6×10π V≈113.04 V
故瞬时值表达式为:
e=Emcosωt=36πcos10πt V=113.04cos10πt V
(2)电流的有效值为:
I=$\frac{Im}{\sqrt{2}}$=$\frac{{E}_{m}}{\sqrt{2}(R+r)}$=$\frac{113.04}{\sqrt{2}×(45+5)}$=1.6 A
(3)线圈的周期为:
T=$\frac{2π}{ω}$=0.2s;
0.05=$\frac{T}{4}$;
根据v法拉第电磁感应定律,可得平均感应电动势为:
$\overline{E}$=n$\frac{△Φ}{△t}$=$\frac{nBS}{△t}$
根据闭合电路欧姆定律,平均感应电流为:
$\overline{I}$=$\frac{\overline{E}}{R+r}$=$\frac{nBS}{(R+r)△t}$=$\frac{10×0.2×0.6×0.3}{50×0.05}$=1.44 A
答:(1)从图示位置开始计时线圈中感应电动势的瞬时值表达式e=113.04cos10πt V;
(2)感应电流的有效值1.6A.
(3)从图示位置开始计时0.05s内平均感应电流的大小为1.44A..
点评 本题考查交流电的四值问题,要重点掌握有效值及平均值的计算方法,明确求电压表电流表的示数及功率等问题时,要用到有效值.

 阅读快车系列答案
阅读快车系列答案 在水平支持面上放一个木支架A,在A的竖直杆的下方套有一块环形铁片B,上方固定一个电磁铁C,如图所示.电磁铁C与支架A的总质量为M,铁片B的质量为m.当电磁铁通电时,铁片B被吸起并向上运动,此时支架A对水平支持面的压力F的大小( )
在水平支持面上放一个木支架A,在A的竖直杆的下方套有一块环形铁片B,上方固定一个电磁铁C,如图所示.电磁铁C与支架A的总质量为M,铁片B的质量为m.当电磁铁通电时,铁片B被吸起并向上运动,此时支架A对水平支持面的压力F的大小( )| A. | F=Mg | B. | F=(M+m)g | C. | F>(M+m)g | D. | Mg<F<(M+m)g |
 如图所示,AB为半径R=2m的一段光滑圆糟,A、B两点在同一水平高度上,且AB弧长20cm.将一小球由A点释放,则它运动到B点所用时间为( )
如图所示,AB为半径R=2m的一段光滑圆糟,A、B两点在同一水平高度上,且AB弧长20cm.将一小球由A点释放,则它运动到B点所用时间为( )| A. | $\frac{1}{2π}$$\sqrt{\frac{R}{g}}$ | B. | $\sqrt{\frac{2πR}{g}}$ | C. | π$\sqrt{\frac{R}{g}}$ | D. | 2π$\sqrt{\frac{R}{g}}$ |
 一理想变压器的原线圈连接一只交流电流表,副线圈接入电路的匝数可以通过触头Q调节,如图所示.在副线圈两输出端连接灯泡L、定值电阻R0和滑动变阻器R,在原线圈上加一电压为U的交变电流,则( )
一理想变压器的原线圈连接一只交流电流表,副线圈接入电路的匝数可以通过触头Q调节,如图所示.在副线圈两输出端连接灯泡L、定值电阻R0和滑动变阻器R,在原线圈上加一电压为U的交变电流,则( )| A. | 保持Q位置不动,将P向上滑动时,灯泡变亮,电流表的读数变大 | |
| B. | 保持Q位置不动,将P向上滑动时,灯泡变暗,电流表的读数变小 | |
| C. | 保持P位置不动,将Q向上滑动时,灯泡变亮,电流表的读数变大 | |
| D. | 保持P位置不动,将Q向上滑动时,灯泡变暗,电流表的读数变小 |
 在“验证机械能守恒定律”的实验中,质量为m的重锤拖着纸带下落,在此过程中,打点计时器在纸带上打出一系列的点,在纸带上选取 5个相邻计数点A、B、C、D和E,相邻计数点时间间隔为 T,其中O为重锤开始下落时记录的点,各计数点之间的距离如图所示.(当地重力加速度为g)
在“验证机械能守恒定律”的实验中,质量为m的重锤拖着纸带下落,在此过程中,打点计时器在纸带上打出一系列的点,在纸带上选取 5个相邻计数点A、B、C、D和E,相邻计数点时间间隔为 T,其中O为重锤开始下落时记录的点,各计数点之间的距离如图所示.(当地重力加速度为g) 如图所示,真空中有以(r,0)为圆心、半径为r的圆柱形匀强磁场区域,磁场的磁感应强度大小为B,方向垂直于纸面向里,在y=r的上方足够大的范围内,有方向水平向左的匀强电场,电场强度的大小为E,从O点向不同方向发射速率相同的质子,质子的运动轨迹均在纸面内.设质子在磁场中的轨道半径也为r,已知质子的电量为e,质量为m,不计重力及阻力的作用.求:
如图所示,真空中有以(r,0)为圆心、半径为r的圆柱形匀强磁场区域,磁场的磁感应强度大小为B,方向垂直于纸面向里,在y=r的上方足够大的范围内,有方向水平向左的匀强电场,电场强度的大小为E,从O点向不同方向发射速率相同的质子,质子的运动轨迹均在纸面内.设质子在磁场中的轨道半径也为r,已知质子的电量为e,质量为m,不计重力及阻力的作用.求:
 阅读下文,解答下列问题:
阅读下文,解答下列问题: