题目内容
5.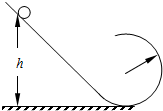 一质量m=2kg的小球从光滑斜面上高h=3.5m处由静止滑下,斜面底端紧接着一个半径R=1m的光滑圆环轨道,如图所示.求:
一质量m=2kg的小球从光滑斜面上高h=3.5m处由静止滑下,斜面底端紧接着一个半径R=1m的光滑圆环轨道,如图所示.求:(1)小球滑至圆环最高点时对环压力的大小;
(2)小球至少应从多高处静止滑下才能越过圆环最高点.
分析 (1)先根据机械能守恒求出小球通过圆环顶点时的速度,再由牛顿第二定律求出圆环对小球的压力,即可得解.
(2)小球恰能通过圆轨道的最高点,重力提供向心力,根据牛顿第二定律列式;整个过程中只有重力做功,机械能守恒,根据机械能守恒定律列方程;最后联立求解即可.
解答 解:(1)小球从静止开始到圆环顶点的过程,由机械能守恒得:
mg(h-2R)=$\frac{1}{2}$mv2
在圆环顶点时,对小球,有:
mg+N=m$\frac{{v}^{2}}{R}$,
代入数据解得:N=40N,
根据牛顿第三定律得:小球滑至圆环顶点时对环的压力:N′=N=40N
(2)设小球从离最低点高度为H的地方下滑,在轨道最高点的速度为v′,则:
mg(H-2R)=$\frac{1}{2}$mv′2,
在最高点由重力提供向心力:
mg=m$\frac{v{′}^{2}}{R}$
由上两式得:H=2.5R=2.5m;
则小球应从大于等于2.5m范围内由静止滑下才能使小球在圆环上越过最高点;
答:(1)小球滑至圆环顶点时对环的压力为40N;
(2)小球应从大于等于2.5m范围内由静止滑下才能越过最高点.
点评 本题关键是明确小球的运动规律,然后根据牛顿第二定律和机械能守恒定律列方程联立求解;关键在于明确小球恰好经过最高点时重力恰好提供向心力.

练习册系列答案
相关题目
15.用中子轰击${\;}_{92}^{235}$U原子核发生裂变反应,其裂变方程为${\;}_{92}^{235}$U+${\;}_{0}^{1}$n→X+${\;}_{38}^{90}$Sr+10${\;}_{0}^{1}$n,则下列叙述正确的是( )
| A. | X原子核中含有54个中子 | |
| B. | X原子核中含有136个核子 | |
| C. | 裂变时释放能量,出现质量亏损,裂变后的总质量将减少 | |
| D. | 裂变时释放能量,出现质量亏损,裂变后的总质量数将减少 |
16.关于物体重力势能增加量的下列几种说法,正确的是( )
| A. | 物体只受到拉力作用竖直向上加速运动,拉力做功1J,物体重力势能增加量也是1J | |
| B. | 物体只受到拉力作用竖直向上匀速运动,拉力做功1J,物体重力势能增加量可能是1J | |
| C. | 没有摩擦时物体沿斜面运动克服重力做功1J,物体重力势能增加量是1J | |
| D. | 物体运动时重力做功是-1J,物体重力势能增加量是-1J |
13. 如图所示,在皮带传动装置中,主动轮A和从动轮B半径之比为RA:RB=1:2,皮带与轮之间无相对滑动,则下列关于两轮边缘上点的角速度和线速度大小之间的关系,正确的是( )
如图所示,在皮带传动装置中,主动轮A和从动轮B半径之比为RA:RB=1:2,皮带与轮之间无相对滑动,则下列关于两轮边缘上点的角速度和线速度大小之间的关系,正确的是( )
 如图所示,在皮带传动装置中,主动轮A和从动轮B半径之比为RA:RB=1:2,皮带与轮之间无相对滑动,则下列关于两轮边缘上点的角速度和线速度大小之间的关系,正确的是( )
如图所示,在皮带传动装置中,主动轮A和从动轮B半径之比为RA:RB=1:2,皮带与轮之间无相对滑动,则下列关于两轮边缘上点的角速度和线速度大小之间的关系,正确的是( )| A. | vA:vB=1:2 | B. | vA:vB=2:1 | C. | ωA:ωB=1:2 | D. | ωA:ωB=2:1 |
10.下列关于惯性的说法正确的是( )
| A. | 物体只有在静止或做匀速直线运动时才有惯性 | |
| B. | 乘坐汽车时系好安全带可减小乘客的惯性 | |
| C. | 速度大的汽车不容易停下来,说明汽车运动时的惯性比静止时的惯性大 | |
| D. | “月兔”探测器在地球上和月球上的惯性一样大 |
10.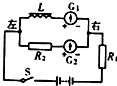 在如图所示的电路中,L是电感线圈,R1、R2是电阻,两个灵敏电流表G1和G2的零点都在刻度盘中央,当电流从“+”接线柱流入时,指针向右摆,电流从“-”接线柱流入时,指针向左摆,在电路接通后再断开的瞬间,下列说法符合实际的情况是( )
在如图所示的电路中,L是电感线圈,R1、R2是电阻,两个灵敏电流表G1和G2的零点都在刻度盘中央,当电流从“+”接线柱流入时,指针向右摆,电流从“-”接线柱流入时,指针向左摆,在电路接通后再断开的瞬间,下列说法符合实际的情况是( )
 在如图所示的电路中,L是电感线圈,R1、R2是电阻,两个灵敏电流表G1和G2的零点都在刻度盘中央,当电流从“+”接线柱流入时,指针向右摆,电流从“-”接线柱流入时,指针向左摆,在电路接通后再断开的瞬间,下列说法符合实际的情况是( )
在如图所示的电路中,L是电感线圈,R1、R2是电阻,两个灵敏电流表G1和G2的零点都在刻度盘中央,当电流从“+”接线柱流入时,指针向右摆,电流从“-”接线柱流入时,指针向左摆,在电路接通后再断开的瞬间,下列说法符合实际的情况是( )| A. | G1、G2表的指针都向右摆 | |
| B. | G1、G2表的指针都向左摆 | |
| C. | G1表的指针向右摆,G2表的指针向左摆 | |
| D. | G1表的指针向左摆,G2表的指针向右摆 |
11.下面是一些有关高中物理实验的描述,其中正确的是 ( )
| A. | 在“研究匀变速直线运动”实验中,不需要平衡摩擦力 | |
| B. | 在“验证机械能守恒定律”的实验中,必须用天平测物体的质量 | |
| C. | 在“探究力的平行四边形定则”的实验中,在同一次实验中橡皮条拉长的结点O位置可以不同 | |
| D. | 在用橡皮筋“探究功与速度变化的关系”的实验中不需要直接求出合外力做的功 | |
| E. | 在用欧姆表“×10”挡测量电阻时发现指针偏转角太小,应该换“×1”挡进行测量 |