题目内容
19.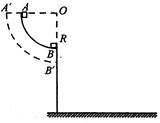 如图所示,半径可变的四分之一光滑圆弧轨道置于竖直平面内,轨道的末端B处切线水平,现将一小物体从轨道顶端A处由静止释放.若保持圆心的位置不变,改变圆弧轨道的半径(不超过圆心离地的高度).半径越大,小物体( )
如图所示,半径可变的四分之一光滑圆弧轨道置于竖直平面内,轨道的末端B处切线水平,现将一小物体从轨道顶端A处由静止释放.若保持圆心的位置不变,改变圆弧轨道的半径(不超过圆心离地的高度).半径越大,小物体( )| A. | 落地时的速度越大 | |
| B. | 平抛的水平位移越大 | |
| C. | 到圆弧轨道最低点时加速度越大 | |
| D. | 落地时的速度与竖直方向的夹角越大 |
分析 (1)根据动能定理知B点的速度和落地速度,结合牛顿第二定律求出加速度的大小;根据加速度表达式表示加速度.
(2)根据高度,结合位移时间公式求出平抛运动的时间,根据速度时间公式求出落地时的竖直分速度,结合平行四边形定则求出落地的速度方向.
解答 解:A、根据动能定理知mgH=$\frac{1}{2}$mv2知总高度不变,末速度大小不变,故A错误;
B、根据平抛运动规律知
h=$\frac{1}{2}$gt2,
x=v0t
mgR=$\frac{1}{2}$mv${\;}_{0}^{2}$
得x=$\sqrt{2gR}$$•\sqrt{\frac{2(H-R)}{g}}$=2$\sqrt{R(H-R)}$,平抛运动的水平位移随R增大后减小,故B错误;
C、到圆弧轨道最低点时加速度a=$\frac{{v}_{0}^{2}}{R}$=2g,故加速度大小与R无关,故C错误;
D、小滑块落地时竖直分速度vy=gt
设与水平方向的夹角为θ,有tanθ=$\frac{gt}{{v}_{0}}$=$\frac{g•\sqrt{\frac{2(H-R)}{g}}}{\sqrt{2gR}}$=$\sqrt{\frac{H-R}{R}}$,R越大,落地时的速度与竖直方向的夹角越大,故D正确;
故选:D
点评 本题考查了圆周运动和平抛运动的综合,知道平抛运动在水平方向和竖直方向上的运动规律和圆周运动向心力的来源是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.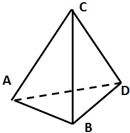 如图所示,正四面体所有棱长都相等长度为a,A、B、C、D是其四个顶点,现在B、D两点分别固定电量均为q的正负点电荷,静电力常量为k,下列说法正确的是( )
如图所示,正四面体所有棱长都相等长度为a,A、B、C、D是其四个顶点,现在B、D两点分别固定电量均为q的正负点电荷,静电力常量为k,下列说法正确的是( )
 如图所示,正四面体所有棱长都相等长度为a,A、B、C、D是其四个顶点,现在B、D两点分别固定电量均为q的正负点电荷,静电力常量为k,下列说法正确的是( )
如图所示,正四面体所有棱长都相等长度为a,A、B、C、D是其四个顶点,现在B、D两点分别固定电量均为q的正负点电荷,静电力常量为k,下列说法正确的是( )| A. | C点的场强大小为$\sqrt{3}$$\frac{kq}{{a}^{2}}$ | |
| B. | A、C两点的场强方向相同 | |
| C. | A、C两点电势相同 | |
| D. | 将一正电荷从A点沿直线移动到C点,电场力先做正功后做负功 |
10.下列物理量的单位是“法拉”的是( )
| A. | 电流 | B. | 电容 | C. | 电场强度 | D. | 磁感应强度 |
14.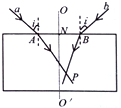 如图所示,直线OO′与上下表面平行的玻璃砖垂直且与其上表面交于N点.a,b两种单色光以相同的入射角i射到玻璃砖的上表面,入射点A、B到N点的距离相等,经折射后两束光相交于图中的P点.下列说法正确的是( )
如图所示,直线OO′与上下表面平行的玻璃砖垂直且与其上表面交于N点.a,b两种单色光以相同的入射角i射到玻璃砖的上表面,入射点A、B到N点的距离相等,经折射后两束光相交于图中的P点.下列说法正确的是( )
 如图所示,直线OO′与上下表面平行的玻璃砖垂直且与其上表面交于N点.a,b两种单色光以相同的入射角i射到玻璃砖的上表面,入射点A、B到N点的距离相等,经折射后两束光相交于图中的P点.下列说法正确的是( )
如图所示,直线OO′与上下表面平行的玻璃砖垂直且与其上表面交于N点.a,b两种单色光以相同的入射角i射到玻璃砖的上表面,入射点A、B到N点的距离相等,经折射后两束光相交于图中的P点.下列说法正确的是( )| A. | a光在玻璃中的折射率比b光的大 | |
| B. | a光在玻璃中的传播速度比b光的小 | |
| C. | 对同一双缝干涉装置,a光的条纹间距比b光的小 | |
| D. | 增大i(i<90°),a.b光总能从玻璃砖的下表面射出 |
9.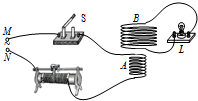 如图,多匝线圈A与电键、滑动变阻器相连后接入M、N间的交流电源,B线圈与小灯泡L相连.下列说法正确的是( )
如图,多匝线圈A与电键、滑动变阻器相连后接入M、N间的交流电源,B线圈与小灯泡L相连.下列说法正确的是( )
 如图,多匝线圈A与电键、滑动变阻器相连后接入M、N间的交流电源,B线圈与小灯泡L相连.下列说法正确的是( )
如图,多匝线圈A与电键、滑动变阻器相连后接入M、N间的交流电源,B线圈与小灯泡L相连.下列说法正确的是( )| A. | L发光时,电路中发生了自感现象 | |
| B. | L发光时,A线圈的输入功率等于B线圈的输出功率 | |
| C. | 只有在闭合电键瞬间,L才能发光 | |
| D. | 若闭合电键后L不发光,将滑动变阻器滑片左移后,L可能会发光 |
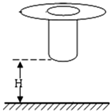 将一个小圆环瓷片保持环面平行地面从高处由静止释放,小瓷片直接撞击地面不被摔坏的最大释放高度为hm.若将该圆环瓷片套在圆柱体的上端,瓷片可沿圆柱体下滑,但瓷片与圆柱体间的滑动摩擦力是瓷片重力的μ倍(μ>1),如图所示,现将该装置从下端距地面H高处由静止释放,瓷片撞击地面时速度最大且恰好不被摔坏.已知瓷片、圆柱体与瓷片下落过程中均受空气阻力的作用,空气阻力恒为自身重力的k倍(k>1),重力加速度为g,圆柱体与地面碰撞后速度立即变为零且保持竖立.求:
将一个小圆环瓷片保持环面平行地面从高处由静止释放,小瓷片直接撞击地面不被摔坏的最大释放高度为hm.若将该圆环瓷片套在圆柱体的上端,瓷片可沿圆柱体下滑,但瓷片与圆柱体间的滑动摩擦力是瓷片重力的μ倍(μ>1),如图所示,现将该装置从下端距地面H高处由静止释放,瓷片撞击地面时速度最大且恰好不被摔坏.已知瓷片、圆柱体与瓷片下落过程中均受空气阻力的作用,空气阻力恒为自身重力的k倍(k>1),重力加速度为g,圆柱体与地面碰撞后速度立即变为零且保持竖立.求: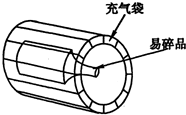 用密封性好、充满气体的塑料袋包裹易碎品,如图所示.充气袋四周被挤压时,假设袋内气体与外界无热交换,则袋内气体体积减小(填“增大”、“不 变”或“减小”),内能增大(填“增大”、“不变”或“减小,’),压强增大(填“增大”、“不变”或“减小,’),对外界做负功(填“做正功”、“做负 功”或“不做功”)
用密封性好、充满气体的塑料袋包裹易碎品,如图所示.充气袋四周被挤压时,假设袋内气体与外界无热交换,则袋内气体体积减小(填“增大”、“不 变”或“减小”),内能增大(填“增大”、“不变”或“减小,’),压强增大(填“增大”、“不变”或“减小,’),对外界做负功(填“做正功”、“做负 功”或“不做功”)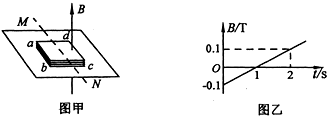
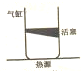 如图,一个横截面积为S的导热气缸直立放置,质量为m的楔形活塞下方封闭一定质量的理想气体,活塞上方与大气相通,气缸底与热源接触.被封闭气体温度为T0,体积为V0,经过热源缓慢加热,气体温度升高到T1时,用卡子卡住活塞,使之不能上升,热源继续加热,使气体温度升高到T2.已知大气压为P0,不计活塞与缸壁的摩擦.求:
如图,一个横截面积为S的导热气缸直立放置,质量为m的楔形活塞下方封闭一定质量的理想气体,活塞上方与大气相通,气缸底与热源接触.被封闭气体温度为T0,体积为V0,经过热源缓慢加热,气体温度升高到T1时,用卡子卡住活塞,使之不能上升,热源继续加热,使气体温度升高到T2.已知大气压为P0,不计活塞与缸壁的摩擦.求: