题目内容
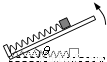
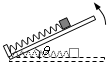
如图在水平板的左端有一固定挡板,挡板上连接一轻质弹簧.紧贴弹簧放一质量为m的滑块,此时弹簧处于自然长度.已知滑块与板的动摩擦因数为
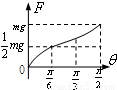
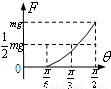
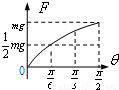
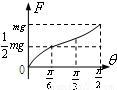
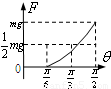
,最大静摩擦力等于滑动摩擦力.现将板的右端缓慢抬起(板与水平面的夹角为θ),直到板竖直,此过程中弹簧弹力的大小F随夹角θ的变化关系可能是( )
| ||
| 3 |
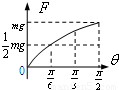
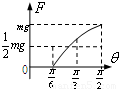
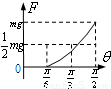
A.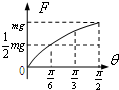 | B.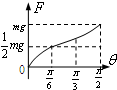 | C.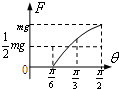 | D.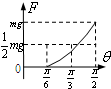 |

设板与水平面的夹角为α时,滑块相对于板刚要滑动,则由mgsinα=μmgcosα得 tanα=
,α=
则θ在0-
范围内,弹簧处于原长,弹力F=0
当板与水平面的夹角大于α时,滑块相对板缓慢滑动,由平衡条件得F=mgsinθ-μmgcosθ=
sin(θ-β),其中tanβ=-μ,说明F与θ正弦形式的关系.当θ=
时,F=mg.
故选C
| ||
| 3 |
| π |
| 6 |
则θ在0-
| π |
| 6 |
当板与水平面的夹角大于α时,滑块相对板缓慢滑动,由平衡条件得F=mgsinθ-μmgcosθ=
| mg | ||
|
| π |
| 2 |
故选C

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
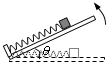 (2013?甘肃模拟)如图在水平板的左端有一固定挡板,挡板上连接一轻质弹簧.紧贴弹簧放一质量为m的滑块,此时弹簧处于自然长度.已知滑块与板的动摩擦因数为
(2013?甘肃模拟)如图在水平板的左端有一固定挡板,挡板上连接一轻质弹簧.紧贴弹簧放一质量为m的滑块,此时弹簧处于自然长度.已知滑块与板的动摩擦因数为 ,最大静摩擦力等于滑动摩擦力.现将板的右端缓慢抬起(板与水平面的夹角为θ),直到板竖直,此过程中弹簧弹力的大小F随夹角θ的变化关系可能是( )
,最大静摩擦力等于滑动摩擦力.现将板的右端缓慢抬起(板与水平面的夹角为θ),直到板竖直,此过程中弹簧弹力的大小F随夹角θ的变化关系可能是( )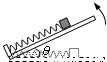
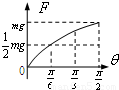

 ,最大静摩擦力等于滑动摩擦力.现将板的右端缓慢抬起(板与水平面的夹角为θ),直到板竖直,此过程中弹簧弹力的大小F随夹角θ的变化关系可能是( )
,最大静摩擦力等于滑动摩擦力.现将板的右端缓慢抬起(板与水平面的夹角为θ),直到板竖直,此过程中弹簧弹力的大小F随夹角θ的变化关系可能是( )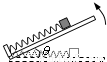

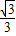 ,最大静摩擦力等于滑动摩擦力.现将板的右端缓慢抬起(板与水平面的夹角为θ),直到板竖直,此过程中弹簧弹力的大小F随夹角θ的变化关系可能是( )
,最大静摩擦力等于滑动摩擦力.现将板的右端缓慢抬起(板与水平面的夹角为θ),直到板竖直,此过程中弹簧弹力的大小F随夹角θ的变化关系可能是( )