��Ŀ����
3��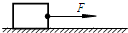 ��ͼ����Ϊm=10kg��ľ�����ˮƽ�ذ��ϣ���F=60N���ҵ�ˮƽ�����������ɾ�ֹ��ʼ��ֱ���˶�������ʱ��t=2.0s����������֪ľ����ذ�֮��Ķ�Ħ������Ϊ��=0.2����ȡg=10m/s2����
��ͼ����Ϊm=10kg��ľ�����ˮƽ�ذ��ϣ���F=60N���ҵ�ˮƽ�����������ɾ�ֹ��ʼ��ֱ���˶�������ʱ��t=2.0s����������֪ľ����ذ�֮��Ķ�Ħ������Ϊ��=0.2����ȡg=10m/s2������1������F��ľ�����Ĺ�Ϊ���٣�
��2������������5.0sʱ��ľ���ڵذ���λ��Ϊ���
��3������ȥ����F�����̽�F������������ľ���ϣ�F�Ĵ�С���䣬��������3.0s��������ٶ�Ϊ���
���� ��1����ţ�ٵڶ�������ļ��ٶȣ����˶�ѧ��ʽ���2s�ڵ�λ�ƣ�����W=Fx�����������
��2����ó�ȥ������ļ��ٶȣ��жϼ��ٵ�������ʱ�䣬�����˶�ѧ��ʽ���λ��
��3�����������ļ��ٶȣ��жϳ����ٵ�������ʱ�䣬Ȼ��������˶�����������ٶ�
��� �⣺��1����ţ�ٵڶ����ɿɵ�F-��mg=ma
���a=4m/s2
2s�ڵ�λ��Ϊx=$\frac{1}{2}a{t}^{2}=\frac{1}{2}��4��{2}^{2}m=8m$
����������ΪW=Fx=60��8J=480J
��2��2sĩ���ٶ�Ϊv=at=8m/s
��ȥ������ļ��ٶ�Ϊ$a��=\frac{��mg}{m}=��g=2m/{s}^{2}$
�ٶȼ���������ʱ��Ϊ$t��=\frac{v}{a��}=\frac{8}{2}s=4s��5s$
�ʼ����˶���λ��Ϊ$x��=\frac{{v}^{2}}{2a��}=\frac{{8}^{2}}{2��2}m=16m$
��ͨ����λ��X=x+x��=24m
��3�����Ϸ�����ʱ�ļ��ٶ�Ϊ$a��=\frac{F+��mg}{m}=\frac{60+0.2��10��10}{10}m/{s}^{2}=8m/{s}^{2}$
�ٶȼ���������ʱ��Ϊt��=$\frac{v}{a��}=\frac{8}{8}s=1s$
�ٶȼ������������˶�����3sĩ���ٶ�Ϊv��=a��t=4��2m/s=8m/s
�𣺣�1������F��ľ�����Ĺ�Ϊ480J
��2������������5.0sʱ��ľ���ڵذ���λ��Ϊ24m
��3������ȥ����F�����̽�F������������ľ���ϣ�F�Ĵ�С���䣬��������3.0s��������ٶ�Ϊ8m/s
���� ������Ҫ������������˶����ؼ���ץס������˶����̣����ú��˶�ѧ��ʽ������ý�

 ÿ�α���ϵ�д�
ÿ�α���ϵ�д� ��ѧ����ϵ�д�
��ѧ����ϵ�д�| A�� | ���ݵ糡ǿ�ȵĶ���ʽE=$\frac{F}{q}$���糡��ij��ĵ糡ǿ�Ⱥ���̽��ɵĵ����ɷ��� | |
| B�� | �糡������ĵ��Ʋ���ȷ���ģ������������ѡȡ�й� | |
| C�� | ��������е��ɵ糡ǿ�ȹ�ʽE=k$\frac{Q}{{r}^{2}}$���糡��ij��糡ǿ�Ⱥͳ�Դ��ɵĵ����� | |
| D�� | �糡��ij��ĵ�����ο�ƽ���ѡȡ�й� |
| A�� | ���Ӽ�����������Ӽ�������Ҳ������ | |
| B�� | ���Ӽ������������ƽ��������С | |
| C�� | ѹǿ��С��ͬʱ���ϴӳ�ˮ���������� | |
| D�� | ѹǿ��С�����Ȳ�����Ҳ������ |
| A�� | �����ڹ⻬ˮƽ�����������˶�ʱ���������˶���ƽ�����ܲ��� | |
| B�� | ��������������ʱ����������ܲ�һ������ | |
| C�� | �¶���ȵ���������Ӵ������Ǹ��Ե�����һ������ | |
| D�� | �����ڲ�ij�����ӵĶ�������ʱ��������¶Ȳ�һ������ |
| A�� | 1m3ͭ������ԭ����Ŀ��$\frac{��{N}_{A}}{M}$ | B�� | 1kgͭ������ԭ����Ŀ�Ǧ�NA | ||
| C�� | һ��ͭԭ�ӵ������ǣ�$\frac{M}{{N}_{A}}$��kg | D�� | һ��ͭԭ��ռ�е�����ǣ�$\frac{M}{��{N}_{A}}$��m3 |
| A�� | ��ֱ����Ͷ������������˶�����ֱ�����˶� | |
| B�� | ��ֱ�����˶����ȱ���ֱ���˶�������ٶ�Ϊ�������ٶ�g | |
| C�� | ��ֱ�����˶����Կ������������˶�������ֱ���˶��������˶��ĺ��˶� | |
| D�� | �������������˶�һ��ʱ���������˶��ɿ�����ֱ�����˶� |
 ��ͼ��ʾ������A����������B�ϣ�����B���ڹ⻬ˮƽ���ϣ�����A��B�������ֱ�ΪmA=6kg��mB=2kg������A��B��Ķ�Ħ��������=0.2����ʼʱˮƽ��F����������A����F=10N���˺�������F��������45N�Ĺ����У�gȡ10m/s2����������
��ͼ��ʾ������A����������B�ϣ�����B���ڹ⻬ˮƽ���ϣ�����A��B�������ֱ�ΪmA=6kg��mB=2kg������A��B��Ķ�Ħ��������=0.2����ʼʱˮƽ��F����������A����F=10N���˺�������F��������45N�Ĺ����У�gȡ10m/s2����������| A�� | ����F��12 Nʱ������������־�ֹ״̬ | |
| B�� | ������ʼ��û������˶� | |
| C�� | �������������ʼ��������˶� | |
| D�� | �����忪ʼû������˶�������������12 Nʱ����ʼ��Ի��� |
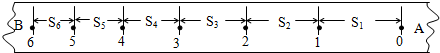
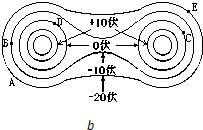 ��ͼ��ʾ����һ������ƽ�д���Բ����ֱƽ��ĵ����ߣ���ͼ�б���˸������ߵĵ�����ֵ������
��ͼ��ʾ����һ������ƽ�д���Բ����ֱƽ��ĵ����ߣ���ͼ�б���˸������ߵĵ�����ֵ������