Question

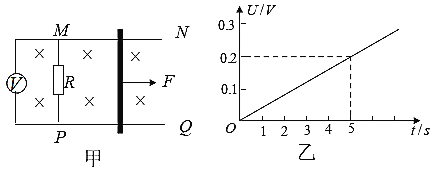
【题目】如图，从阴极K发射的热电子，重力和初速均不计，通过加速电场后，沿图示虚线垂直射入匀强磁场区，磁场区域足够长，宽度为L＝2.5cm。已知加速电压为U＝182V，磁感应强度 ，电子的电量 ，电子质量。求：

（1)电子在磁场中的运动半径R

(2)电子在磁场中运动的时间t(结果保留)

(3)若加速电压大小可以改变，其他条件不变，为使电子在磁场中的运动时间最长，加速电压U应满足什么条件？

Answer 1

【答案】（1） （2） （3）

【解析】试题分析：（1）应用动能定理电子解出电子穿出电场时的速度．电子进入磁场后发生偏转，做匀速圆周运动，由洛伦兹力提供向心力，根据牛顿第二定律求解在磁场中的运动半径R．

（2）先根据圆周运动的知识求得电子在磁场中运动的周期T．画出轨迹，由几何知识求出电子在磁场中运动轨迹所对应的圆心角θ，由t=T求解在磁场中运动的时间t．

（3）为使电子在磁场中的运动时间最长，电子轨迹对应的圆心角必须最大，最大圆心角为180°，轨迹恰好与磁场右边界相切，求得轨迹半径，根据上题的结果即可求解．

解：（1）加速电场中由动能定理得；

eU=mv2﹣0

解得：v===8×106m/s

磁场中做圆周运动，由牛顿第二定律得：

evB=

解得：R==m=0.05m

（2）磁场中运动的周期 T==s=×10﹣7s

由几何关系 sinθ==

则 θ=30°

故电子在磁场中运动的时间为：t=T==×10﹣7s

（3）电子在磁场中的运动时间最长时，圆心角 θ=180°

当运动轨迹恰与磁场右界相切时，R=L=2.5cm=0.025m

依题意有R≤0.025m

由 R=和v=得：U=

代入解得：U≤45.5V

（1）电子在磁场中的运动半径R是0.05m．

（2）电子在磁场中运动的时间t是×10﹣7s．

（3）为使电子在磁场中的运动时间最长，加速电压U应满足的条件是：U≤45.5V．