题目内容
如图所示,圆柱形区域的横截面在没有磁场的情况下,带电粒子(不计重力)以某一初速度沿截面直径方向入射时,穿过此区域的时间为t;若该区域加沿轴线方向的匀强磁场,磁感应强度为B,带电粒子仍以同一初速度沿截面直径入射,粒子飞出此区域时,速度方向偏转了π/3,根据上述条件可求得的物理量为( )
| A.带电粒子的初速度 |
| B.带电粒子在磁场中运动的半径 |
| C.带电粒子在磁场中运动的周期 |
| D.带电粒子的比荷 |
CD
解析试题分析:无磁场时,带电粒子做匀速直线运动,设圆柱形区域磁场的半径为R0,则 ;而有磁场时,带电粒子做匀速圆周运动,由半径公式可得:
;而有磁场时,带电粒子做匀速圆周运动,由半径公式可得: ;由几何关系得,圆磁场半径与圆轨道半径的关系:
;由几何关系得,圆磁场半径与圆轨道半径的关系: ;联式可得:
;联式可得: ;设粒子在磁场中的运动时间t0,粒子飞出此区域时,速度方向偏转60°角,则由周期公式可得:
;设粒子在磁场中的运动时间t0,粒子飞出此区域时,速度方向偏转60°角,则由周期公式可得: ;由于不知圆磁场的半径,因此带电粒子的运动半径也无法求出,以及初速度无法求.故选:CD.
;由于不知圆磁场的半径,因此带电粒子的运动半径也无法求出,以及初速度无法求.故选:CD.
考点:带电粒子在匀强磁场中的运动。

处于同一平面内的两根长直导线中通有方向相反大小不同的电流,这两根导线把它们所在的平面分成a、b、c三个区域,如图所示,则磁感强度为零的区域 
| A.可能出现在a区 | B.可能出现在b区 |
| C.可能出现在c区 | D.a区、b区、c区都有可能 |
如图所示,一半径为R的圆形区域内有垂直于纸面向里的匀强磁场,一质量为 ,电量为
,电量为 的正电荷(重力忽略不计)以速度
的正电荷(重力忽略不计)以速度 沿正对着圆心o的方向射入磁场,从磁场中射出时速度方向改变了
沿正对着圆心o的方向射入磁场,从磁场中射出时速度方向改变了 角。磁场的磁感应强度大小为
角。磁场的磁感应强度大小为
A. | B. |
C. | D.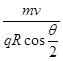 |
如图是某离子速度选择器的原理示意图,在一半径为R 的绝缘圆柱形筒内有磁感应强度为B的匀强磁场,方向平行于轴线.在圆柱形筒上某一直径两端开有小孔M、N,现有一束速率不同、比荷均为k的正、负离子,从M孔以α角入射,一些具有特定速度的离子未与筒壁碰撞而直接从N孔射出(不考虑离子间的作用力和重力).则从N孔射出的离子( )
| A.是正离子,速率为kBR/cos α |
| B.是正离子,速率为kBR/sin α |
| C.是负离子,速率为kBR/sin α |
| D.是负离子,速率为kBR/cos α |
如图所示,用两根轻细金属丝将质量为m,长为 的金属棒ab悬挂在c.d两处,置于匀强磁场内。当棒中通以从a到b的电流I后,两悬线偏离竖直方向θ角处于平衡状态.为了使棒平衡在该位置上,所需的最小磁场的磁感应强度的大小.方向是( )
的金属棒ab悬挂在c.d两处,置于匀强磁场内。当棒中通以从a到b的电流I后,两悬线偏离竖直方向θ角处于平衡状态.为了使棒平衡在该位置上,所需的最小磁场的磁感应强度的大小.方向是( )
A. ,竖直向上 ,竖直向上 |
B. ,竖直向下 ,竖直向下 |
C.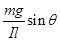 ,平行悬线向下 ,平行悬线向下 |
D.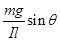 ,平行悬线向上 ,平行悬线向上 |




 越大
越大