题目内容
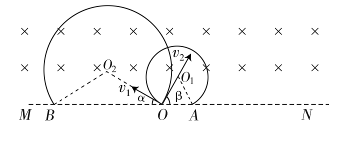
如图所示,直线MN上方存在着垂直纸面向里、磁感应强度为B的匀强磁场,质量为m、电荷量为-q(q>0)的粒子1在纸面内以速度v1=v0从O点射入磁场,其方向与MN的夹角α=30°;质量为m、电荷量为+q的粒子2在纸面内以速度v2= v0也从O点射入磁场,其方向与MN的夹角β=60°角。已知粒子1、2同时到达磁场边界的A、B两点(图中未画出),不计粒子的重力及粒子间的相互作用。
v0也从O点射入磁场,其方向与MN的夹角β=60°角。已知粒子1、2同时到达磁场边界的A、B两点(图中未画出),不计粒子的重力及粒子间的相互作用。
(1)求两粒子在磁场边界上的穿出点A、B之间的距离d;
(2)求两粒子进入磁场的时间间隔Δt;
(3)若MN下方有平行于纸面的匀强电场,且两粒子在电场中相遇,其中的粒子1做直线运动。求电场强度E的大小和方向。
(1)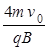 (2)
(2)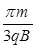 (3)
(3)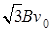 ,方向与MN成30°角斜向右上。
,方向与MN成30°角斜向右上。
解析试题分析:(1)粒子在匀强磁场中作匀速圆周运动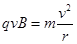
故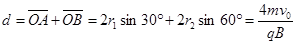
(2)粒子1圆周运动的圆心角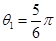 ,
, 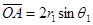
粒子2圆周运动的圆心角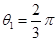 ,
, 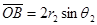
粒子圆周运动的周期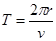
粒子1在匀强磁场中运动的时间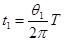
粒子2在匀强磁场中运动的时间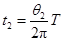
所以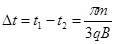
(3)由题意,电场强度的方向应与粒子1穿出磁场的方向平行。
a.若电场强度的方向与MN成30°角斜向右上,则粒子1做匀加速直线运动,粒子2做类平抛运动。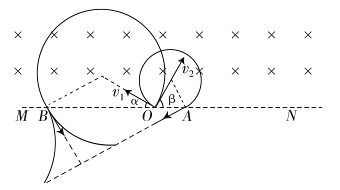
Eq="ma"
ABcos30°=v1t+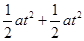
ABsin30°=v2t
解得E=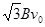
b.若电场强度的方向与MN成30°角斜向左下,则粒子1做匀减速直线运动,粒子2做类平抛运动。
Eq="ma"
ABcos30°=v1t-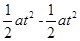
ABsin30°=v2t
解得E=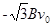 ,假设不成立。
,假设不成立。
综上所述,电场强度的大小E=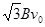 ,方向与MN成30°角斜向右上。
,方向与MN成30°角斜向右上。
考点:带电粒子在电场及磁场中的运动;

 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
 C,相距20cm,则它们之间的相互作用力为__________N,在两者连线的中点处,电场强度大小为__________N/C.(k=" 9.0" ×109N m2/C2)
C,相距20cm,则它们之间的相互作用力为__________N,在两者连线的中点处,电场强度大小为__________N/C.(k=" 9.0" ×109N m2/C2) cm,板长
cm,板长 cm,一个质量为
cm,一个质量为 kg的带电微粒,以
kg的带电微粒,以 m/s的水平初速度从两板间正中央射入,如图所示,取
m/s的水平初速度从两板间正中央射入,如图所示,取 m/s2。
m/s2。
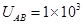 V时,微粒恰好不发生偏转,求微粒的电量和电性。
V时,微粒恰好不发生偏转,求微粒的电量和电性。 的取值范围?
的取值范围?


 =2×108 C/kg的正电荷从坐标为(0,1)的A点处由静止释放.电荷所受的重力忽略不计.
=2×108 C/kg的正电荷从坐标为(0,1)的A点处由静止释放.电荷所受的重力忽略不计.