题目内容
18.在光滑水平地面上,原来静止的物体在水平力F作用下,经过时间t,通过位移l后,动量变为p,动能变为Ek.在力F作用下,若这个物体( )| A. | 经过时间为2t,则其动量将等于2p | B. | 经过位移为2l,则其动量将等于2p | ||
| C. | 经过位移为2l,则其动能将等于2Ek | D. | 经过时间为2t,则其动能将等于2Ek |
分析 (1)由动量定理求出动量,然后由动能与动量的关系求出动能;
(2)由动能定理求出物体的动能,由动能与动量的关系求出动量.
解答 解:由题意可知,经过时间t、通过位移l后,动量为p、动能为Ek,由动量定理可知:P=Ft,由动能定理得:EK=Fl,设物体质量为m;
AD、当时间为2t时,动量P′=F•2t=2Ft=2P,物体的动能:EK′=$\frac{p{′}^{2}}{2m}$=$\frac{(2p)^{2}}{2m}$=4$\frac{{p}^{2}}{2m}$=4EK,故A正确,D错误;
BC、当位移为2l时,物体的动能EK′=F•2l=2Fl=2EK,物体的动量:P′=$\sqrt{2m{E}_{K}′}$=$\sqrt{2m×2{E}_{K}}$=$\sqrt{2}$P,故B错误,C正确;
故选:AC.
点评 本题考查了求动能与动量,应用动能定理与动量定理即可正确解题,解题时要注意应用动能与动量的数量关系.

练习册系列答案
相关题目
3. 如图所示,半径为r的圆形区域内有匀强磁场,磁场方向垂直纸面向里,磁场的磁感应强度随时间均匀增大,其变化率为$\frac{△B}{△t}$=k;纸面内的平行金属导轨ab、cd与磁场边界相切于O、O′点,边长ab=2bc,导轨两端接有电阻均为R的两灯泡,构成回路,金属导轨的电阻忽略不计.则回路中( )
如图所示,半径为r的圆形区域内有匀强磁场,磁场方向垂直纸面向里,磁场的磁感应强度随时间均匀增大,其变化率为$\frac{△B}{△t}$=k;纸面内的平行金属导轨ab、cd与磁场边界相切于O、O′点,边长ab=2bc,导轨两端接有电阻均为R的两灯泡,构成回路,金属导轨的电阻忽略不计.则回路中( )
 如图所示,半径为r的圆形区域内有匀强磁场,磁场方向垂直纸面向里,磁场的磁感应强度随时间均匀增大,其变化率为$\frac{△B}{△t}$=k;纸面内的平行金属导轨ab、cd与磁场边界相切于O、O′点,边长ab=2bc,导轨两端接有电阻均为R的两灯泡,构成回路,金属导轨的电阻忽略不计.则回路中( )
如图所示,半径为r的圆形区域内有匀强磁场,磁场方向垂直纸面向里,磁场的磁感应强度随时间均匀增大,其变化率为$\frac{△B}{△t}$=k;纸面内的平行金属导轨ab、cd与磁场边界相切于O、O′点,边长ab=2bc,导轨两端接有电阻均为R的两灯泡,构成回路,金属导轨的电阻忽略不计.则回路中( )| A. | 产生感应电动势,但无感应电流 | B. | 感应电流方向为abcda | ||
| C. | 感应电流的大小为$\frac{kπ{r}^{2}}{2R}$ | D. | 感应电流的大小为$\frac{2kπ{r}^{2}}{R}$ |
7. 游乐场的过山车可以底朝上在圆轨道上运行,游客却不会掉下来.我们把这种情形抽象为如图所示的模型:弧形轨道的下端与竖直圆轨道相接,使小球从弧形轨道上端从静止滚下后,进入圆轨道下端并沿圆轨道运动.如果h可调,圆轨道的半径为R,不考虑摩擦等阻力,为使小球不脱离轨道,则h的取值范围是( )
游乐场的过山车可以底朝上在圆轨道上运行,游客却不会掉下来.我们把这种情形抽象为如图所示的模型:弧形轨道的下端与竖直圆轨道相接,使小球从弧形轨道上端从静止滚下后,进入圆轨道下端并沿圆轨道运动.如果h可调,圆轨道的半径为R,不考虑摩擦等阻力,为使小球不脱离轨道,则h的取值范围是( )
 游乐场的过山车可以底朝上在圆轨道上运行,游客却不会掉下来.我们把这种情形抽象为如图所示的模型:弧形轨道的下端与竖直圆轨道相接,使小球从弧形轨道上端从静止滚下后,进入圆轨道下端并沿圆轨道运动.如果h可调,圆轨道的半径为R,不考虑摩擦等阻力,为使小球不脱离轨道,则h的取值范围是( )
游乐场的过山车可以底朝上在圆轨道上运行,游客却不会掉下来.我们把这种情形抽象为如图所示的模型:弧形轨道的下端与竖直圆轨道相接,使小球从弧形轨道上端从静止滚下后,进入圆轨道下端并沿圆轨道运动.如果h可调,圆轨道的半径为R,不考虑摩擦等阻力,为使小球不脱离轨道,则h的取值范围是( )| A. | h>$\frac{5}{2}R$ | B. | h>R | C. | h<R | D. | R<h<$\frac{5}{2}R$ |
8.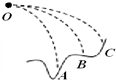 在同一点O抛出的三个质量相同的物体做平抛运动的轨迹如图所示.设三个物体做平抛运动的时间分别为tA、tB、tC,抛出时的机械能为EA、EB、EC,则( )
在同一点O抛出的三个质量相同的物体做平抛运动的轨迹如图所示.设三个物体做平抛运动的时间分别为tA、tB、tC,抛出时的机械能为EA、EB、EC,则( )
 在同一点O抛出的三个质量相同的物体做平抛运动的轨迹如图所示.设三个物体做平抛运动的时间分别为tA、tB、tC,抛出时的机械能为EA、EB、EC,则( )
在同一点O抛出的三个质量相同的物体做平抛运动的轨迹如图所示.设三个物体做平抛运动的时间分别为tA、tB、tC,抛出时的机械能为EA、EB、EC,则( )| A. | EA>EB>EC,tA>tB>tC | B. | EA>EB>EC,tA=tB=tC | ||
| C. | EA<EB<EC,tA>tB>tC | D. | EA<EB<EC,tA<tB<tC |

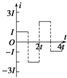
 如图所示,在平面直角坐标系xOy的第二和第四象限分布着垂直于纸面向里的匀强磁场B1=B,在第三象限分布着垂直于纸面向外的匀强磁场B2=2B.现将一直角扇形闭合导线框OPQ以恒定角速度ω绕过O点垂直于坐标平面的轴沿顺时针方向匀速转动.t=0时刻线框处在图示位置,设电流逆时针方向为正方向.则图所示导线框中的电流随时间变化的图象正确的是( )
如图所示,在平面直角坐标系xOy的第二和第四象限分布着垂直于纸面向里的匀强磁场B1=B,在第三象限分布着垂直于纸面向外的匀强磁场B2=2B.现将一直角扇形闭合导线框OPQ以恒定角速度ω绕过O点垂直于坐标平面的轴沿顺时针方向匀速转动.t=0时刻线框处在图示位置,设电流逆时针方向为正方向.则图所示导线框中的电流随时间变化的图象正确的是( )


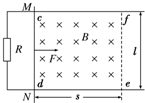 如图所示,光滑的平行金属导轨水平放置,电阻不计,导轨间距为l,左侧接一阻值为R的电阻.区域cdef内存在垂直轨道平面向下的有界匀强磁场,磁场宽度为s.一质量为m、电阻为r的金属棒MN置于导轨上,与导轨垂直且接触良好,受到F=0.5v+0.4(N)(v为金属棒速度)的水平外力作用,从磁场的左边界由静止开始运动,测得电阻两端电压随时间均匀增大.(已知:l=1m,m=1kg,R=0.3Ω,r=0.2Ω,s=1m)
如图所示,光滑的平行金属导轨水平放置,电阻不计,导轨间距为l,左侧接一阻值为R的电阻.区域cdef内存在垂直轨道平面向下的有界匀强磁场,磁场宽度为s.一质量为m、电阻为r的金属棒MN置于导轨上,与导轨垂直且接触良好,受到F=0.5v+0.4(N)(v为金属棒速度)的水平外力作用,从磁场的左边界由静止开始运动,测得电阻两端电压随时间均匀增大.(已知:l=1m,m=1kg,R=0.3Ω,r=0.2Ω,s=1m)