题目内容
13.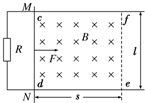 如图所示,光滑的平行金属导轨水平放置,电阻不计,导轨间距为l,左侧接一阻值为R的电阻.区域cdef内存在垂直轨道平面向下的有界匀强磁场,磁场宽度为s.一质量为m、电阻为r的金属棒MN置于导轨上,与导轨垂直且接触良好,受到F=0.5v+0.4(N)(v为金属棒速度)的水平外力作用,从磁场的左边界由静止开始运动,测得电阻两端电压随时间均匀增大.(已知:l=1m,m=1kg,R=0.3Ω,r=0.2Ω,s=1m)
如图所示,光滑的平行金属导轨水平放置,电阻不计,导轨间距为l,左侧接一阻值为R的电阻.区域cdef内存在垂直轨道平面向下的有界匀强磁场,磁场宽度为s.一质量为m、电阻为r的金属棒MN置于导轨上,与导轨垂直且接触良好,受到F=0.5v+0.4(N)(v为金属棒速度)的水平外力作用,从磁场的左边界由静止开始运动,测得电阻两端电压随时间均匀增大.(已知:l=1m,m=1kg,R=0.3Ω,r=0.2Ω,s=1m)(1)判断该金属棒在磁场中是否做匀加速直线运动;
(2)求加速度的大小和磁感应强度B的大小;
(3)若撤去外力后棒的速度v随位移x的变化规律满足v=v0-$\frac{{B}^{2}{l}^{2}}{m(R+r)}$x,且棒在运动到ef处时恰好静止,则外力F作用的时间为多少?
(4)若在棒未出磁场区域时撤出外力,画出棒在整个运动过程中速度随位移变化所对应的各种可能的图线.
分析 (1)根据感应电动势、欧姆定律得到电阻R两端的电压与金属棒速度v的关系式,根据速度均匀增大,分析棒的运动情况.
(2)根据牛顿第二定律求出棒的加速度表达式,根据加速度是恒量,解得加速度a和磁感应强度B.
(3)根据R两端的电压U均匀增大,分析金属棒的运动性质.U均匀增大,v均匀增大,金属棒做匀加速运动,由运动学公式得出金属棒匀加速运动的位移和速度与时间的关系式.撤去外力后,由题v=v0-$\frac{{B}^{2}{l}^{2}}{m(R+r)}$x,得到匀加速运动的末速度与减速运动位移的关系式,联立求解时间t.
(4)作出棒在整个运动过程中速度v随位移x变化的各种可能的图线
解答 解:(1)金属棒做匀加速直线运动,因为R两端电压U∝I∝E∝v,U随时间均匀增大,即v随时间均匀增大.所以加速度为恒量.
(2)根据牛顿第二定律有:F-$\frac{{B}^{2}{l}^{2}v}{R+r}$=ma,将F=0.5v+0.4代入,得:(0.5-$\frac{{B}^{2}{l}^{2}}{R+r}$)v+0.4=a
因为加速度为恒量,与v无关,所以a=0.4m/s2
且有 0.5-$\frac{{B}^{2}{l}^{2}}{R+r}$=0,代入数据得:B=0.5T.
(3)设外力F作用时间为t,
x1=$\frac{1}{2}$at2,v0=$\frac{{B}^{2}{l}^{2}}{m(R+r)}$x2=at,x1+x2=s,所以 $\frac{1}{2}$at2+$\frac{m(R+r)}{{B}^{2}{l}^{2}}$at=s,
代入数据得 0.2t2+0.8t-1=0
解方程得 t=1s或t=-5s(舍去).
(4)可能图线如下: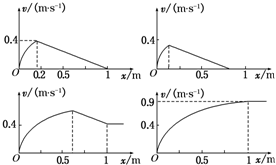
答:
(1)金属棒在磁场中做匀加速直线运动;
(2)加速度的大小是0.4m/s2,磁感应强度B的大小0.5T;
(3)外力F作用的时间为1s;
(4)画出棒在整个运动过程中速度随位移变化所对应的各种可能的图线如上图所示.
点评 根据物理规律找出物理量的关系,通过已知量得出未知量.要善于对物体过程分析和进行受力分析,运用牛顿第二定律结合运动学公式解决问题.

 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案| A. | $\frac{3}{2}$v | B. | $\frac{4}{3}$v | C. | $\frac{3}{4}$v | D. | $\frac{2}{3}$v |
| A. | 原子中带正电的部分体积很小 | |
| B. | 电子是原子产的组成部分 | |
| C. | 原子是一个正、负电荷均匀分布的球 | |
| D. | α粒子带正电 |
| A. | 只跟恒星的质量有关 | B. | 只跟行星的质量有关 | ||
| C. | 跟行星恒星的质量都有关 | D. | 跟行星恒星的质量都没关 |
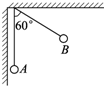 如图所示,真空中两个相同的小球带有等量同种电荷,质量均为0.1g,分别用10cm长的绝缘细线悬挂于绝缘天花板的一点,当平衡时B球偏离竖直方向60°,A竖直悬挂且与绝缘墙接触(g取10m/s2).静电力常量K=9.0×109 N•m2/C2.下列说法正确的是( )
如图所示,真空中两个相同的小球带有等量同种电荷,质量均为0.1g,分别用10cm长的绝缘细线悬挂于绝缘天花板的一点,当平衡时B球偏离竖直方向60°,A竖直悬挂且与绝缘墙接触(g取10m/s2).静电力常量K=9.0×109 N•m2/C2.下列说法正确的是( )| A. | 小球的带电荷量为3.33×10-8 C | B. | 墙壁受到的压力为8.7×10-4 N | ||
| C. | A球受到细线的拉力为1.0×10-3 N | D. | B球受到的拉力为1.5×10-3 N |
| A. | 经过时间为2t,则其动量将等于2p | B. | 经过位移为2l,则其动量将等于2p | ||
| C. | 经过位移为2l,则其动能将等于2Ek | D. | 经过时间为2t,则其动能将等于2Ek |
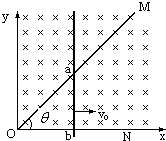 如图所示,顶角θ=60°的金属导轨MON固定在水平面内,导轨处在方向竖直、磁感应强度为B的匀强磁场中.一根与ON垂直的导体棒在水平外力作用下以恒定速度v0沿导轨MON向右滑动,导体棒的质量为m,导体棒单位长度的电阻均为r,导体棒与导轨接触点的a和b,导体棒在滑动过程中始终保持与导轨良好接触.t=0时,导体棒位于顶角O处,金属导轨MON的电阻不计且光滑.求:
如图所示,顶角θ=60°的金属导轨MON固定在水平面内,导轨处在方向竖直、磁感应强度为B的匀强磁场中.一根与ON垂直的导体棒在水平外力作用下以恒定速度v0沿导轨MON向右滑动,导体棒的质量为m,导体棒单位长度的电阻均为r,导体棒与导轨接触点的a和b,导体棒在滑动过程中始终保持与导轨良好接触.t=0时,导体棒位于顶角O处,金属导轨MON的电阻不计且光滑.求: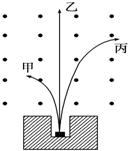 图是放射源放出的三种射线经过匀强磁场后分裂成三束,
图是放射源放出的三种射线经过匀强磁场后分裂成三束,