题目内容
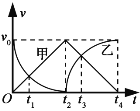
【题目】如图甲所示，斜面AB粗糙，倾角为θ= 30o，其底端A处有一垂直斜面的挡板，一质量为m=2 kg的滑块从B点处由静止释放，滑到底端A处与挡板碰撞并反弹到最高点C处，已知滑块与挡板碰撞时能量损失了19%，滑块的v-t图象如图乙所示，重力加速度g＝ 10m/s2．
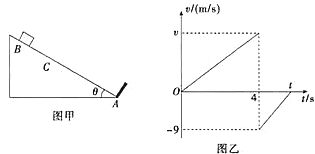
(1)求v-t图象中的v、t的值；
(2)求滑块与斜面间的动摩擦因数μ；
(3)若滑块与挡板碰撞无能量损失，求滑块整个运动过程中通过的总路程s．
【答案】（1）v=10m/s,t=5.2s （2）
（3）s=40m
【解析】
试题（1）由图象知滑块反弹速率为为：v2=9m/s，
反弹时能量为：Ek2=
mv22=×2×81=81J；
因碰撞时能量损失19%；即滑块下滑到A 处时能量为：
；
而：EK1=mv2；
代入数据解得：v=10m/s；
又因v=at1；
解得：
；
由牛顿第二定律知滑块下滑时有：mgsinθ-μmgcosθ=ma1；
反弹上滑时有：mgsinθ+μmgcosθ=ma2；
而v2=a2t2
联立并代入数据得：t2=1．2s
所以有：t=4+1．2=5．2s；
（2）因mgsinθ-μmgcosθ=ma1；
代入数据得；
（3）由
可知AB长为：
由能量守恒知：mgLsinθ-μmgcosθs=0；
代入数据解得：s=40m；
【题目】某同学设计了一个探究加速度a与物体所受合力F及质量m关系的实验，图（a）为实验装置简图。（交流电的频率为50Hz）
（1）图（b）为某次实验得到的纸带，根据纸带可求出小车的加速度大小为___m/s2。（保留二位有效数字）
（2）保持砂和砂桶质量不变，改变小车质量m，分别得到小车加速度a与质量m及对应的1/m，数据如下表：
实验次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
小车加速度a/m·s—2 | 1.90 | 1.72 | 1.49 | 1.25 | 1.00 | 0.75 | 0.50 | 0.30 |
小车质量m/kg | 0.25 | 0.29 | 0.33 | 0.40 | 0.50 | 0.71 | 1.00 | 1.67 |
| 4.00 | 3.45 | 3.03 | 2.50 | 2.00 | 1.41 | 1.00 | 0.60 |
请在方格坐标纸中画出
图线_____，并从图线求出小车加速度a与质量倒数
之间的关系式是______________。
（3）保持小车质量不变，改变砂和砂桶质量，该同学根据实验数据作出了加速度a随合力F的变化图线如图（c）所示。该图线不通过原点，其主要原因是_______________。
