题目内容
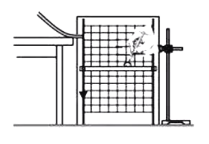
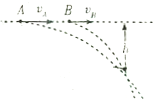
【题目】如图所示，将A.B两个小球从同一水平线上相距为L的两个位置分別以速度vA,,vB，同时水平抛出，不计空气阻力，当两球在空中的下落高度为h时，两球相遇。如果仅将两球水平抛出的速度都变为原来2倍，则两球在空中相遇时下落的高度h'为
A. h B. 
C. 
h D. 
h
【答案】D
【解析】
平抛运动在水平方向上做匀速直线运动，抓住两球的水平位移不变，结合初速度的变化得出两球从抛出到相遇经过的时间，再由竖直分位移公式分析两球相遇点的位置．
两球同时抛出，竖直方向上做自由落体运动，相等时间内下降的高度相同，始终在同一水平面上，根据L=vAt-vBt知，L不变，当两球的抛出速度都变为原来的2倍，则两球从抛出到相遇经过的时间为t/2，根据h=
gt2，知两球下落的高度是
h，则两球在空中相遇时下落的高度h'为h．故D正确，ABC错误。故选D。
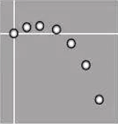
优学名师名题系列答案
【题目】某同学在“探究小车速度随时间变化的规律”的实验中，所用交流电的周期为T =0.02s。打点计时器记录了被小车拖动的纸带的运动情况，在纸带上确定出A、B、C、D、E、F、G共7个计数点。其相邻点间的距离（可依次用字母x1、x2、x3、x4、x5、x6表示）如图所示，每两个相邻的计数点之间还有4个打印点未画出。
（1）试根据纸带上各个计数点间的距离，计算出打下B、F两个点时小车的瞬时速度，并将这两个速度值填入下表（要求保留2位有效数字）。
速度 | vB | vC | vD | vE | vF |
数值（m/s） | 0.50 | 0.61 | 0.73 |
（2）将B、C、D、E、F各个时刻的瞬时速度标在直角坐标系中，并画出小车的瞬时速度随时间变化的关系图线。
（3）可由所画v—t图像求出小车加速度为____________m/s2(计算结果要求：保留小数点后面二位数字）。
（4）本题亦可不利用v—t图像求小车加速度，请写出计算小车加速度的表达式：
（用字母x1、x2、x3、x4、x5、x6和T表示）。
