题目内容
2. 用一根长1m的轻质细绳将一幅质量为1kg的画框对称悬挂在墙壁上,已知绳能承受的最大张力10N,为使绳不断裂,画框上两个钉的间距最大为(g取10m/s2)( )
用一根长1m的轻质细绳将一幅质量为1kg的画框对称悬挂在墙壁上,已知绳能承受的最大张力10N,为使绳不断裂,画框上两个钉的间距最大为(g取10m/s2)( )| A. | $\frac{\sqrt{2}}{2}$m | B. | $\frac{\sqrt{3}}{2}$m | C. | $\frac{1}{2}m$ | D. | $\frac{\sqrt{3}}{4}$m |
分析 将重力按照力的效果进行分解,即沿两细线的方向分解,求出绳子即将断开时的临界角度(两细线夹角)即可得出画框上两个挂钉的最大间距.
解答 解:一个大小方向确定的力分解为两个等大的力时,合力在分力的角平分线上,且两分力的夹角越大,分力越大,因而当绳子拉力达到F=10N的时候,绳子间的张角最大,为120°,此时两个挂钉间的距离最大;
画框受到重力和绳子的拉力,三个力为共点力,受力如图.
绳子与竖直方向的夹角为θ=60°,绳子长为L0=1m,
则有mg=2Fcosθ,两个挂钉的间距离L=2•$\frac{{L}_{0}}{2}$sinθ,
解得L=$\frac{\sqrt{3}}{2}$m;
故选:B
点评 熟练应用力的合成和分解以及合成与分解中的一些规律,是解决本题的根本.

练习册系列答案
相关题目
15.已知万有引力常量G=6.67×10-11Nm2/kg2,假设质量分别为50kg和60kg两个人距离为1km时,他们之间的相互吸引力约等于( )
| A. | 600N | B. | 500N | C. | 2×10-13N | D. | 2×10-6N |
14.如图所示,放在电梯地板上的货箱,在随电梯加速上升过程中( )


| A. | 电梯对货箱做的功等于货箱动能的增量 | |
| B. | 电梯对货箱做的功等于货箱增加的机械能 | |
| C. | 货箱处于超重状态 | |
| D. | 货箱处于失重状态 |
 如图,用长L的绝缘细线栓住一个质量为m,带电量为q的小球,线的另一端栓在水平向右的匀强电场中,开始时把小球、线拉到和O在同一水平面上的A点(线拉直),让小球由静止开始释放,当摆线摆到与水平线成60°角到达B点时,球的速度正好为零,求:
如图,用长L的绝缘细线栓住一个质量为m,带电量为q的小球,线的另一端栓在水平向右的匀强电场中,开始时把小球、线拉到和O在同一水平面上的A点(线拉直),让小球由静止开始释放,当摆线摆到与水平线成60°角到达B点时,球的速度正好为零,求: 带有等量异种电荷的两个平行金属板A和B水平放置,相距为d,一个带正电的油滴P悬浮在两板的正中央处于静止,油滴的质量为m,电荷量为q,如图所示,在油滴的正上方距A板距离为d处有一质量也为m的带正电油滴N,油滴N由静止释放,可穿过A板上的小孔,进入两金属板间,已知油滴N能与油滴P相碰,且结合成大油滴(仍可视为质点),大油滴刚好运动到B板,但又不与金属板B相碰.求:
带有等量异种电荷的两个平行金属板A和B水平放置,相距为d,一个带正电的油滴P悬浮在两板的正中央处于静止,油滴的质量为m,电荷量为q,如图所示,在油滴的正上方距A板距离为d处有一质量也为m的带正电油滴N,油滴N由静止释放,可穿过A板上的小孔,进入两金属板间,已知油滴N能与油滴P相碰,且结合成大油滴(仍可视为质点),大油滴刚好运动到B板,但又不与金属板B相碰.求: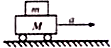 如图所示,小车质量M为2.0kg.与水平地面阻力忽略不计,物体质量m为0.5kg,g取10m/s2,设滑动摩擦力等于最大静摩擦力,物体始终在小车上,则:
如图所示,小车质量M为2.0kg.与水平地面阻力忽略不计,物体质量m为0.5kg,g取10m/s2,设滑动摩擦力等于最大静摩擦力,物体始终在小车上,则:
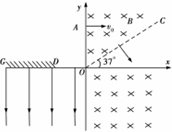 如图所示,在坐标系xOy的第一象限内斜线OC的上方存在垂直纸面向里的匀强磁场,磁感应强度为B,第四象限内存在磁感应强度大小未知,方向垂直纸面向里的匀强磁场,第三象限内存在沿y轴负方向的匀强电场,在x轴负半轴上有一接收屏GD,GD=20D=d,现有一带电粒子(不计重力)从y轴上的A点,以初速度v0水平向右垂直射入匀强磁场,恰好垂直OC射出,并从x轴上的P点(未画出)进入第四象限内的匀强磁场,粒子经磁场偏转后又垂直y轴进入匀强电场并被接收屏接收,已知OC与x轴的夹角为37°,OA=$\frac{4}{5}$d,求:
如图所示,在坐标系xOy的第一象限内斜线OC的上方存在垂直纸面向里的匀强磁场,磁感应强度为B,第四象限内存在磁感应强度大小未知,方向垂直纸面向里的匀强磁场,第三象限内存在沿y轴负方向的匀强电场,在x轴负半轴上有一接收屏GD,GD=20D=d,现有一带电粒子(不计重力)从y轴上的A点,以初速度v0水平向右垂直射入匀强磁场,恰好垂直OC射出,并从x轴上的P点(未画出)进入第四象限内的匀强磁场,粒子经磁场偏转后又垂直y轴进入匀强电场并被接收屏接收,已知OC与x轴的夹角为37°,OA=$\frac{4}{5}$d,求: