题目内容
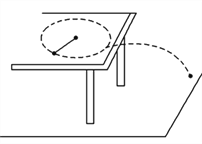
【题目】如图所示,一根长0.1m的细线,一端系着一个质量为0.18kg的小球,拉住线的另一端,使小球在光滑的水平桌面上做匀速圆周运动,使小球的转速很缓慢地增加,当小球的角速度增加到开始时角速度的3倍时,细线断开,线断开前的瞬间线受到的拉力比开始时大40 N,求:
(1)线断开前的瞬间,线受到的拉力大小;
(2)线断开的瞬间,小球运动的线速度;
(3)如果小球离开桌面时,速度方向与桌边缘的夹角为60°,桌面高出地面0.8 m,求小球飞出后的落地点距桌边缘的水平距离。
【答案】(1) F=45N(6分) (2)![]() (6分) (3)
(6分) (3)![]() (6分)
(6分)
【解析】试题分析:(1)线的拉力等于向心力,设开始时角速度为ω0,向心力是F0,线断开的瞬间,角速度为ω,线的拉力是FT。 已知ω=3ω0
F0=mω02R ①
FT=mω2R ②
由①②得FT=9F0③
又因为FT=F0+40N ④
由③④得FT=45N ⑤
(2)设线断开时速度为v ,则![]() ⑥
⑥
代入数据得v=5m/s
(3)设桌面高度为h,小球落地经历时间为t,落地点与飞出桌面点的水平距离为x。
则![]() ⑦
⑦
x=vt=2m ⑧
则小球飞出后的落地点到桌边线的水平距离为l=x·sin60°=1.73 m。

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目