题目内容
9.跳伞员常常采用“加速自由降落”(即AFF)的方法跳伞.如果一个质量为50kg的运动员在3658m的高度从悬停的直升飞机跳出,降落40s时速度达到50m/s,然后打开降落伞,减速下降,安全着陆.假设加速下落过程为匀加速直线运动,g取10m/s2.求:(1)加速下落过程空气对跳伞员的平均阻力的大小f.
(2)跳伞员离地面高度多少时打开降落伞?
分析 根据速度时间公式求出加速下落过程中的加速度,结合牛顿第二定律求出平均阻力的大小.
根据速度位移公式求出匀加速运动的位移,结合总高度求出打开降落伞时离地的高度.
解答 解:(1)加速下落过程中的加速度a=$\frac{v}{t}=\frac{50}{40}m/{s}^{2}=1.25m/{s}^{2}$,
根据牛顿第二定律得,mg-f=ma,
解得f=mg-ma=500-50×1.25N=437.5N.
(2)加速降落的位移为h,$h=\frac{{v}^{2}}{2a}=\frac{5{0}^{2}}{2×1.25}m=1000m$.
开伞时的高度为H,H=H0-h=3658-1000m=2658m.
答:(1)加速下落过程空气对跳伞员的平均阻力的大小为437.5N.
(2)跳伞员离地面高度2658m时打开降落伞.
点评 本题考查了牛顿第二定律和运动学公式的基本运用,通过速度时间公式求出加速度是解决本题的关键,知道加速度是联系力学和运动学的桥梁.

练习册系列答案
相关题目
19.如图甲所示,沿波的传播方向上有间距均为1m的六个质点a、b、c、d、e、f,均静止在各自的平衡位置,t=0时刻振源a从平衡位置竖直向上做简谐运动,其振动图象如图乙所示,形成的简谐横波以1m/s的速度水平向右传播,则下列说法正确的是( )
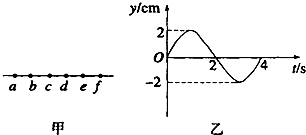
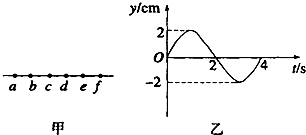
| A. | 这列波的波长为4m | |
| B. | 0~3s质点b运动路程为4cm | |
| C. | 4~5s质点c的加速度在减小 | |
| D. | 6s时质点e的速度为1m/s水平向右 | |
| E. | 此六质点都振动起来后,质点a的运动方向始终与质点c的运动方向相反 |
17.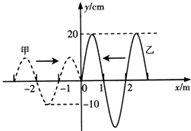 如图,沿同一弹性绳相向传播甲、乙的两列简谐横波,波长相等,振幅分别为10cm、20cm,在某时刻恰好传到坐标原点.则两列波相遇迭加后( )
如图,沿同一弹性绳相向传播甲、乙的两列简谐横波,波长相等,振幅分别为10cm、20cm,在某时刻恰好传到坐标原点.则两列波相遇迭加后( )
 如图,沿同一弹性绳相向传播甲、乙的两列简谐横波,波长相等,振幅分别为10cm、20cm,在某时刻恰好传到坐标原点.则两列波相遇迭加后( )
如图,沿同一弹性绳相向传播甲、乙的两列简谐横波,波长相等,振幅分别为10cm、20cm,在某时刻恰好传到坐标原点.则两列波相遇迭加后( )| A. | 不可能产生稳定的干涉图象 | B. | 在x=2 m的质点振动始终减弱 | ||
| C. | 在x=0.5 m的质点振幅为零 | D. | 坐标原点的振幅为30cm |
4.关于分子动理论的规律,下列说法正确的是( )
| A. | 扩散现象说明物质的分子在做永不停息的无规则运动 | |
| B. | 压缩气体时气体会表现出抗拒压缩的力是由于气体分子间存在斥力的缘故 | |
| C. | 两个分子距离减小时,分子间引力和斥力都在增大 | |
| D. | 两个分子间的距离为r0时,分子势能为0 |
1.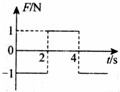 静止在光滑水平面上的物体,受到水平拉力F的作用,拉力F随时间t变化的图象如图所示,则下列说法中正确的是( )
静止在光滑水平面上的物体,受到水平拉力F的作用,拉力F随时间t变化的图象如图所示,则下列说法中正确的是( )
 静止在光滑水平面上的物体,受到水平拉力F的作用,拉力F随时间t变化的图象如图所示,则下列说法中正确的是( )
静止在光滑水平面上的物体,受到水平拉力F的作用,拉力F随时间t变化的图象如图所示,则下列说法中正确的是( )| A. | 0~4s内物体的位移为零 | B. | 0~4s内拉力对物体做功为零 | ||
| C. | 4s末物体的动量为零 | D. | 0~4s内拉力对物体冲量为零 |
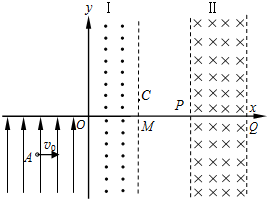 如图所示,在直角坐标系xoy的第一、四象限内存在边界平行y轴的两个有界匀强磁场:垂直纸面向外的匀强磁场Ⅰ、垂直纸面向里的匀强磁场Ⅱ.O、M、P、Q为磁场边界和x轴的交点,OM=MP=L;在第三象限内存在沿y轴正方向的匀强电场.一质量为m,带电量为+q的带电粒子从电场中坐标为(-$\frac{2\sqrt{3}L}{3}$,-L)的A点以速度v0沿+x方向射出,恰好经过原点O射入区域Ⅰ,从C点射出区域Ⅰ,从某点射入区域Ⅱ,射入时速度与+x轴方向成30°角斜向下.经区域Ⅱ的磁场偏转后又从C点进入区域Ⅰ.求:
如图所示,在直角坐标系xoy的第一、四象限内存在边界平行y轴的两个有界匀强磁场:垂直纸面向外的匀强磁场Ⅰ、垂直纸面向里的匀强磁场Ⅱ.O、M、P、Q为磁场边界和x轴的交点,OM=MP=L;在第三象限内存在沿y轴正方向的匀强电场.一质量为m,带电量为+q的带电粒子从电场中坐标为(-$\frac{2\sqrt{3}L}{3}$,-L)的A点以速度v0沿+x方向射出,恰好经过原点O射入区域Ⅰ,从C点射出区域Ⅰ,从某点射入区域Ⅱ,射入时速度与+x轴方向成30°角斜向下.经区域Ⅱ的磁场偏转后又从C点进入区域Ⅰ.求: 如图所示,一细直杆PO始终与水平面夹角为37°,杆可绕过其低端点O的竖直轴OO匀速转动,在杆上端A点处套一小环,当杆静止时,环由A处无初速度沿杆下滑用时1s到达其底端O处,AO距离为1m,最大静摩擦力等于滑动摩擦力,g=10m/s2,sin37°=0.6,cos37°=0.8.求:
如图所示,一细直杆PO始终与水平面夹角为37°,杆可绕过其低端点O的竖直轴OO匀速转动,在杆上端A点处套一小环,当杆静止时,环由A处无初速度沿杆下滑用时1s到达其底端O处,AO距离为1m,最大静摩擦力等于滑动摩擦力,g=10m/s2,sin37°=0.6,cos37°=0.8.求: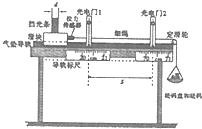 某学习小组利用如图所示的装置验证动能定理.
某学习小组利用如图所示的装置验证动能定理.