题目内容
1．甲、乙两物体先后从同一地点出发，沿一条直线运动，它们的v-t图象如图所示，由图可知（ ）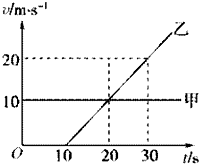
| A． | 甲比乙运动快，且早出发，所以乙能追上甲 | |
| B． | t=20 s时，乙追上了甲 | |
| C． | 在t=20 s之前，甲比乙运动快；在t=20 s之后乙比甲运动快 | |
| D． | 由于乙在t=10 s时才开始运动，所以t=10 s时，甲在乙前面，它们之间的距离为乙追上甲前的最大距离 |
分析 速度图象反映物体速度随时间的变化情况，可直接读出速度的大小；速度图象的“面积”大小等于物体通过的位移大小，根据位移关系即可分析乙何时追上甲；根据速度的大小关系，判断两者距离的变化．
解答 解：A、由图可知：乙在0-10s内速度为零，甲先出发，但乙出发后做匀加速直线运动，甲做匀速直线运动，在t=20s前，甲比乙运动快，在t=20s后，乙比甲运动快，两物体出发地点相同，则乙可以追上甲．故A错误．
BCD、在10-20s内，甲的速度大于乙的速度，甲比乙运动得快，甲在乙的前方，两者距离逐渐增大；20s后，乙的速度大于甲的速度，乙比甲运动得快，两者距离逐渐减小，在t=20s时刻两者距离最大．故BD错误，C正确．
故选：C
点评 本题既考查理解速度图象的能力，也考查分析两物体运动情况的能力，往往当两物体速度相等时，相距最远或最近．
练习册系列答案
相关题目
11．
某金属在光的照射下产生光电效应，其遏止电压Uc与入射光频率v的关系图象如图所示．则由图象可知（ ）
某金属在光的照射下产生光电效应，其遏止电压Uc与入射光频率v的关系图象如图所示．则由图象可知（ ）| A． | 该金属的逸出功等于hν0 | |
| B． | 若已知电子电量e，就可以求出普朗克常量h | |
| C． | 遏止电压是确定的，与照射光的频率无关 | |
| D． | 入射光的频率为2ν0时，产生的光电子的最大初动能为hν0 | |
| E． | 入射光的频率为3ν0时，产生的光电子的最大初动能为hν0 |
在“研究平抛物体运动”实验中，某同学在运动轨迹上只记录了A、B、C三点，并以A点为坐标原点建立了坐标系，各点的坐标如图所示，则物体作平抛运动的初速度大小为$\frac{\sqrt{5}}{10}$m/s，通过B时小球的速度大小为0.5m/s．（重力加速度g取10m/s2）
16．在做”验证力的平行四边形定则”的实验时，橡皮条的一端固定在木板上，用两只弹簧测力计把橡皮条的另一端拉到某一确定的O点，则下列说法中正确的是（ ）
| A． | 实验中，只需记录弹簧测力计的读数和O点的位置 | |
| B． | 实验中，把橡皮条的另一端拉到O点时，两只弹簧测力计之间的夹角必须取90° | |
| C． | 同一次实验中，O点位置不允许变动 | |
| D． | 实验中，要始终将其中一只弹簧测力计沿某一方向拉到最大量程，然后调节另一只弹簧测力计拉力的大小和方向，把橡皮条另一端拉到O点 |
13．以下关于天然放射现象，叙述正确的是（ ）
| A． | 卢瑟福通过α粒子散射实验提出了原子的核式结构模型 | |
| B． | 太阳辐射的能量主要来自太阳内部的热核反应 | |
| C． | 紫外线照射到金属锌板表面时能够发生光电效应，则当增大紫外线的照射强度时，从锌板表面逸出的光电子的最大初动能也随之增大 | |
| D． | 玻尔在研究原子结构中引进了量子化的观念 | |
| E． | 大量的氢原子从n=3的能级向低能级跃迁时只会辐射两种不同频率的光 |
10．
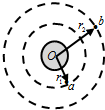如图，若两颗人造卫星a和b均绕地球做匀速圆周运动，a、b到地心O的距离分别为r1、r2，a、b周期大小分别为T1、T2．则（ ）
如图，若两颗人造卫星a和b均绕地球做匀速圆周运动，a、b到地心O的距离分别为r1、r2，a、b周期大小分别为T1、T2．则（ ）| A． | $\frac{{T}_{1}}{{T}_{2}}$=$\sqrt{\frac{{r}_{1}}{{r}_{2}}}$ | B． | $\frac{{T}_{1}}{{T}_{2}}$=$\sqrt{\frac{{r}_{2}}{{r}_{1}}}$ | C． | $\frac{{T}_{1}}{{T}_{2}}$=$\sqrt{\frac{{r}_{1}^{3}}{{r}_{2}^{3}}}$ | D． | $\frac{{T}_{1}}{{T}_{2}}$=$\sqrt{\frac{{r}_{2}^{3}}{{r}_{1}^{3}}}$ |
