Question

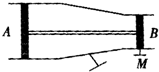如图所示，一传热性能很好的容器，两端是直径不同的两个圆筒，里面各有一个活塞，其横截面积分别为S_A=10cm²和S_B=4cm²，质量分别是M_A=6kg，M_B=4kg．它们之间有一质量不计的轻质细杆相连．两活塞可在筒内无摩擦滑动，但不漏气．在气温是-23℃时，用销子M把B拴住，并把阀门K打开，使容器和大气相通，随后关闭K，此时两活塞间气体体积是300cm²，当气温升到27℃时把销子M拔去．设大气压强为1.10×10⁵Pa不变，容器内气体温度始终和外界相同．求：
（1）刚拔去销子M时两活塞的加速度大小和方向．
（2）活塞在各自圆筒范围内运动一段位移后速度达到最大，这段位移等于多少？?

Answer 1

分析：（1）对于容器中的气体，在K关闭至M拔去前的过程中，是等容变化，列出等式，再运用牛顿第二定律求解．
（2）由于S_A＞S_B，当活塞向左移动时，根据气体方程判断出压强的变化，当减小到与外界压强相等时，加速度为零，这时速度达到最大，根据等温变化列出等式求出这段位移．

解答：解：（1）对于容器中的气体，在K关闭至M拔去前的过程中，是等容变化．
初态：p₁=1.0×10⁵pa，T₁=273-23=250K；
末态：T₂=273+27=300K?
根据查理定律

P1

T1

=

P2

T2

，得：
p₂=1.0×10⁵×

300

250

=1.2×10⁵（Pa）       ①
选取活塞和杆为研究对象，当拔去M时，其受力情况分析如下图所示．
根据牛顿第二定律

a= F m = P2SA-P2SB+P0SB-P0SA mA+mB = (P2-P0)(SA-SB) mA+mB = (1.2×105-1.0×105)×(10×10-4-4×10-4) 6+4 =2m/s2

②
方向：水平向左．?③
（2）由于S_A＞S_B，当活塞向左移动时，气体的体积增大，而气体的温度不变，故气体的压强减小，
从上一问可知活塞和杆的加速度在减小，速度却增大，当减小到与外界压强相等时，加速度为零，这时速度达到最大，利用
初态：p=1.2×10⁵Pa，V=300cm³；
末态：P′=1.0×10⁵Pa，
玻意耳定律：pV=p′V′，所以  
V′=

pV

p′

=

1.2×105×300

1.0×105

=360cm3 ④
设所求移动位移为x，则        V′-V=S_Ax-S_Bx
所以  x=

V′-V

SA-SB

=

360-300

10-4

=10cm⑤
答：（1）刚拔去销子M时两活塞的加速度大小是2m/s²，方向向左．
（2）活塞在各自圆筒范围内运动一段位移后速度达到最大，这段位移等于10cm?

点评：熟练运用气体方程结合牛顿第二定律即可正确解题．利用气态方程解题关键是气体状态要明确，求出各个状态的温度、压强、体积然后列气体状态方程即可求解，尤其注意气体压强的求法．