Question

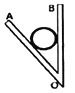
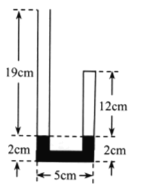
【题目】左右不等高、粗细均匀的玻璃管，左端开口，右端封闭。一段水银柱将一定质量27℃的理想气体封闭在管内，管内水银柱左右两边的液面相平，尺寸如图所示。从左侧沿管壁缓慢注入水银，使右侧水银面上升2cm。大气压强为p0= 75cmHg。求：

(1)注入的水银在管中的长度：

(2)给封闭的气体加热，保证不能有水银溢出管口，求封闭气体温度的最高值。

Answer 1

【答案】(1)19cm；(2)376K

【解析】

(1)对右管封闭气体，p1=p0=75cmHg，V1=12S，V2=(12-2)S，等温变化，有：

p1V1=p2V2 ①

解得

p2=90cmHg②

由两边的压强关系及几何关系，有：

③

（说明：此式之后没有“”而写成p2=p0+h左-h右或其它类似式，不得分。）

代入h右=2cm，解得

h左=17cm ④

注入的水银长度为

l=h左+h右⑤

解得

l=19cm ⑥

(2)注入完水银时，左管水银面离管口距离为19-h左=2cm，故刚好没有水银从左侧管口溢出时，对右管封闭气体，有：

V3=V1=12S，p3=75+19cmHg=94cmHg⑦

与最初状态比较，可认为是等容变化，有

⑧

解法二：与注完水银时比较，⑧式列为同样得分。

其中

T1=t1+273=300K⑨

联立⑦⑧⑨式，解得封闭气体温度的最高值

T3=376K⑩