题目内容
 (2012?盐城二模)两根相距为L的平行光滑金属导轨竖直放置,上端通过导线连接阻值为R的电阻.现有n个条形匀强磁场,方向与导轨平面垂直,磁场区域的宽度为a,间距也为a.一个质量为m、长为L的导体棒(电阻不计)与导轨垂直,在距磁场区域1为a的位置由静止开始释放,此后一直没有离开导轨,且每当进入磁场区域均做匀速运动.求
(2012?盐城二模)两根相距为L的平行光滑金属导轨竖直放置,上端通过导线连接阻值为R的电阻.现有n个条形匀强磁场,方向与导轨平面垂直,磁场区域的宽度为a,间距也为a.一个质量为m、长为L的导体棒(电阻不计)与导轨垂直,在距磁场区域1为a的位置由静止开始释放,此后一直没有离开导轨,且每当进入磁场区域均做匀速运动.求(1)区域Ⅰ的磁感应强度的大小;
(2)导体棒通过磁场区域2的时间;
(3)导体棒从开始下落到穿过磁场区域n的过程中,电阻R上总共产生的电热.
分析:(1)根据机械能守恒求出棒子进入区域Ⅰ的速度,抓住做匀速直线运动,合力为零,求出磁感应强度的大小.
(2)根据匀变速直线运动的速度位移公式求出棒子进入第2个磁场的速度,再根据位移时间公式求出运动的时间.
(3)每次经过磁场区域做匀速直线运动,动能不变,重力势能减小,减小的重力势能转化为电阻R上产生的总热量,根据能量守恒定律求出电热.
(2)根据匀变速直线运动的速度位移公式求出棒子进入第2个磁场的速度,再根据位移时间公式求出运动的时间.
(3)每次经过磁场区域做匀速直线运动,动能不变,重力势能减小,减小的重力势能转化为电阻R上产生的总热量,根据能量守恒定律求出电热.
解答:解:(1)棒子自由下落a,根据机械能守恒得,
v=
进入Ⅰ区域后,导棒做匀速运动,mg=BIL
所以B=
.
(2)可以用磁场外两个连续匀变速运动求速度v2.
v22-02=2g?2a v2=
导体棒通过磁场区域2的时间
t=
=
=
(3)棒在磁场外运动时,机械能守恒,进入后动能不变,势能减小,减小额势能转化为电热.
Q=nmga.
答:(1)区域Ⅰ的磁感应强度的大小B=
.
(2)导体棒通过磁场区域2的时间为
(3)导体棒从开始下落到穿过磁场区域n的过程中,电阻R上总共产生的电热为nmga.
v=
| 2ga |
进入Ⅰ区域后,导棒做匀速运动,mg=BIL
所以B=
|
(2)可以用磁场外两个连续匀变速运动求速度v2.
v22-02=2g?2a v2=
| 4ga |
导体棒通过磁场区域2的时间
t=
| a |
| v2 |
| a | ||
|
| ||
| 2g |
(3)棒在磁场外运动时,机械能守恒,进入后动能不变,势能减小,减小额势能转化为电热.
Q=nmga.
答:(1)区域Ⅰ的磁感应强度的大小B=
|
(2)导体棒通过磁场区域2的时间为
| ||
| 2g |
(3)导体棒从开始下落到穿过磁场区域n的过程中,电阻R上总共产生的电热为nmga.
点评:本题综合考查了导体切割磁感线产生的电动势,机械能守恒定律和能量守恒定律,综合性较强,关键是理清运动过程,选择合适的规律进行求解.

练习册系列答案
相关题目
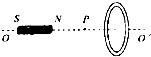 (2012?盐城二模)超导体的电阻为零,如果闭合的超导电路内有电流,这个电流不产生焦耳热,所以不会自行消失.有一超导圆环于图示位置,此时圆环中没有电流.将一根条形磁体沿圆环的中心轴OO’移到P点.以下说法正确的是( )
(2012?盐城二模)超导体的电阻为零,如果闭合的超导电路内有电流,这个电流不产生焦耳热,所以不会自行消失.有一超导圆环于图示位置,此时圆环中没有电流.将一根条形磁体沿圆环的中心轴OO’移到P点.以下说法正确的是( ) (2012?盐城二模)如图所示,A、B两物体静止在粗糙水平面上,其间用一根轻弹簧相连,弹簧的长度大于原长.若再用一个从零开始缓慢增大的水平力F向右拉物体B,直到A即将移动,此过程中,地面对B的摩擦力f1和对A的摩擦力f2的变化情况( )
(2012?盐城二模)如图所示,A、B两物体静止在粗糙水平面上,其间用一根轻弹簧相连,弹簧的长度大于原长.若再用一个从零开始缓慢增大的水平力F向右拉物体B,直到A即将移动,此过程中,地面对B的摩擦力f1和对A的摩擦力f2的变化情况( )