题目内容
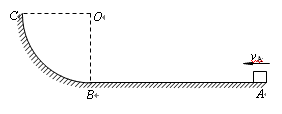
(8分)如图所示,质量M = 4.0kg的木板长L =" 2.0" m,静止在水平地面上,木板与地面间的动摩擦因数为μ1=0.05。木板水平上表面左端静置质量m =" 2.0" kg的小滑块(可视为质点),小滑块与板间的动摩擦因数为μ2 = 0.2。从某时刻开始,用F="5.0" N的水平力一直向右拉滑块,直至滑块滑离木板。设木板与地面间的最大静摩擦力等于滑动摩擦力,取g ="10" m/s2。试求:
(1)此过程中木板的位移大小。
(2)滑块离开木板时的速度大小。
(1) 2.0m (2) 2.0 m/s
解析试题分析:(1)设此过程中木板的加速度为a1,位移大小为x1;滑块的加速度为a2,位移大小为x2。滑块从开始滑动至滑离木板所用时间为t。
由牛顿第二定律和运动学公式得:
对木板:μ2mg –μ1(M + m)g = Ma1 1分
x1 =  a1t2 1分
a1t2 1分
对滑块:F – μ2mg = ma2 1分
x2 = a2t2 1分
a2t2 1分
由几何关系得:x2 – x1 = L 1分
联立以上各式,代入数据解得:
x1 = 2.0m 1分
(2)设滑块滑离木板时的速度为v,由运动学公式得:
v = a2t 1分
代入数据解得:
v =" 2.0" m/s 1分
考点:牛顿第二定律;运动学规律.

练习册系列答案
相关题目
 m的光滑圆弧轨道分别相切于D点和G点,GH与水平面的夹角θ = 37°。过G点、垂直于纸面的竖直平面左侧有匀强磁场,磁场方向垂直于纸面向里,磁感应强度B = 1.25T;过D点、垂直于纸面的竖直平面右侧有匀强电场,电场方向水平向右,电场强度E = 1×104N/C。小物体P1质量m = 2×10-3kg、电荷量q = +8×10-6C,受到水平向右的推力F = 9.98×10-3N的作用,沿CD向右做匀速直线运动,到达D点后撤去推力。当P1到达倾斜轨道底端G点时,不带电的小物体P2在GH顶端静止释放,经过时间t = 0.1s与P1相遇。P1和P2与轨道CD、GH间的动摩擦因数均为
m的光滑圆弧轨道分别相切于D点和G点,GH与水平面的夹角θ = 37°。过G点、垂直于纸面的竖直平面左侧有匀强磁场,磁场方向垂直于纸面向里,磁感应强度B = 1.25T;过D点、垂直于纸面的竖直平面右侧有匀强电场,电场方向水平向右,电场强度E = 1×104N/C。小物体P1质量m = 2×10-3kg、电荷量q = +8×10-6C,受到水平向右的推力F = 9.98×10-3N的作用,沿CD向右做匀速直线运动,到达D点后撤去推力。当P1到达倾斜轨道底端G点时,不带电的小物体P2在GH顶端静止释放,经过时间t = 0.1s与P1相遇。P1和P2与轨道CD、GH间的动摩擦因数均为 =" 0." 5,取g = 10m/s2,sin37° = 0.6,cos37°= 0.8,物体电荷量保持不变,不计空气阻力。求:
=" 0." 5,取g = 10m/s2,sin37° = 0.6,cos37°= 0.8,物体电荷量保持不变,不计空气阻力。求: