题目内容
【题目】如图所示,光滑轨道固定在竖直平面内,其中BCD为细管,AB只有外轨道,AB段和BC段均为半径为R的四分之一圆弧.一小球从距离水平地面高为H(未知)的管口D处静止释放,最后到达A点对轨道的压力大小为mg,并水平抛出落到地面上.求: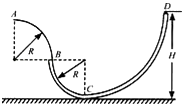
(1)小球到达A点速度vA;
(2)平抛运动的水平位移x;
(3)D点到水平地面的竖直高度H.
【答案】
(1)解:小球恰能够到达A点,由重力提供向心力,根据牛顿第二定律得:
FN+mg=m ![]()
据题得:FN=mg
解得小球到达A点速度为:vA= ![]() .
.
答:小球到达A点速度vA是 ![]() .
.
(2)解:从A点抛出后做平抛运动,则:
水平方向有 x=vAt
竖直方向有 2R= ![]()
联立解得:x=2 ![]() R.
R.
答:平抛运动的水平位移x是2 ![]() R.
R.
(3)解:从D到A运动过程中只有重力做功,机械能守恒,根据机械能守恒定律,则得:
mgH=2mgR+ ![]()
解得:H=3R
答:D点到水平地面的竖直高度H是3R.
【解析】(1)小球到达A点,匀速圆周运动合力提供向心力,根据向心力公式求解vA.
(2)小球离开A点后做平抛运动,运用运动的分解法,由运动学公式求解x.
(3)从D到A运动过程中只有重力做功,机械能守恒,根据机械能守恒定律求出H.
【考点精析】通过灵活运用平抛运动和机械能守恒及其条件,掌握特点:①具有水平方向的初速度;②只受重力作用,是加速度为重力加速度g的匀变速曲线运动;运动规律:平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动;在只有重力(和弹簧弹力)做功的情形下,物体动能和重力势能(及弹性势能)发生相互转化,但机械能的总量保持不变即可以解答此题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目