题目内容
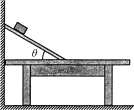
【题目】如图所示,桌子靠墙固定放置,用一块长L1=1.0 m的木板在墙和桌面间架设斜面,桌面距地面H=0.8 m,桌面总长L2=1.5 m,斜面与水平桌面的倾角θ可在0~60°间调节后固定,将质量m=0.2 kg的小物块(可视为质点)从斜面顶端静止释放,物块与斜面间的动摩擦因数μ1=0.05,物块与桌面间的动摩擦因数μ2未知,忽略物块在斜面与桌面交接处的机械能损失,不计空气阻力.(重力加速度取g=10 m/s2;最大静摩擦力等于滑动摩擦力;取sin 37°=0.6,cos 37°=0.8)
(1) 求当θ=30°时,物块在斜面上下滑的加速度的大小;(可以用根号表示)
(2) 当θ增大到37°时,物块恰能停在桌面边缘,求物块与桌面间的动摩擦因数μ2;
(3) μ2取第(2)问中的数值,当θ角为多大时物块落地点与墙面的距离最大,最大距离xm是多少.
【答案】![]()
【解析】
(1) 根据牛顿第二定律,对物体受力分析可得mgsin θ-μ1mgcos θ=ma
代入数据得![]()
(2) 由动能定理得mgL1sin θ-μ1mgL1cos θ-μ2mg(L2-L1cos θ)=0-0
代入数据得μ2=0.8
(3) ![]()
得![]()
当θ=53°时vmax=1 m/s
由于![]() 解得t=0.4 s
解得t=0.4 s
x1=vt=0.4 m
xm=x1+L2=1.9 m

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目