题目内容
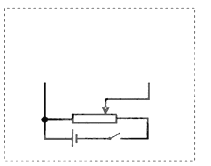
【题目】如图所示,电动机带动下,皮带的传输速度不变,AB为皮带上方的水平段.小物块由静止轻放在皮带左端A处,经过一段时间,物块的速度等于皮带的速度,已知传动轮的半径为R,物块与皮带之间的动摩擦因数为μ.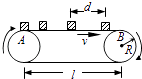
(1)为使物块运动到皮带右端B处时能脱离皮带,皮带的传输速度v和AB段的长度l应分别满足什么条件?
(2)若AB段的长度足够长,已知皮带的传输速度为v,现每隔一段相等的时间就在A处释放一个质量为m的物块,经过一段时间后,皮带右侧相邻物块之间的距离增大到最大值d之后保持不变,直到脱离皮带.求皮带每传输一个物块电动机对皮带做的功,并求电动机对皮带做功的平均功率.
【答案】
(1)
解:物体在B点,重力提供向心力,
由牛顿第二定律得:mg=m ![]() ,解得:v=
,解得:v= ![]() ,
,
物体从静止加速到v过程,由速度位移公式得:
l= ![]() =
= ![]() =
= ![]() ,
,
物体需要满足的条件:v≥ ![]() ,
,
则:l≥ ![]() ;
;
(2)
解:物体获得的动能:EK= ![]() mv2,
mv2,
物体在加速阶段:x1= ![]() ,t1=
,t1= ![]() ,
,
传送带位移:x2= ![]() ,
,
产生的内能:Q=μmg(x2﹣x1),
解得:Q= ![]() mv2,
mv2,
则皮带每传输一个物块电动机对皮带做的功:
W=Q+EK= ![]() mv2+
mv2+ ![]() mv2=mv2,
mv2=mv2,
释放物体的时间间隔:t2= ![]() ,
,
电动机对皮带做功的平均功率:
P= ![]() =
= ![]() =
= ![]() ;
;
【解析】(1)由牛顿第二定律求出速度,然后由匀变速直线运动的速度位移公式求出l需要满足的条件.(2)电动机对每一个物块做的功等于系统产生的热量与物块获得的动能,求电动机对物块做的功,然后由功率公式求出功率.
【考点精析】解答此题的关键在于理解向心力的相关知识,掌握向心力总是指向圆心,产生向心加速度,向心力只改变线速度的方向,不改变速度的大小;向心力是根据力的效果命名的.在分析做圆周运动的质点受力情况时,千万不可在物体受力之外再添加一个向心力,以及对动能定理的理解的理解,了解动能定理的表达式是在物体受恒力作用且做直线运动的情况下得出的.但它也适用于变力及物体作曲线运动的情况;功和动能都是标量,不能利用矢量法则分解,故动能定理无分量式.

 阅读快车系列答案
阅读快车系列答案【题目】在“探究小车速度随时间变化规律”的实验时,某同学得到一条用打点计时器打下的纸带如图所示,并在其上取A、B、C、D、E、F、G等7个计数点,每相邻两个计数点间还有4个点,图中没有画出,打点计时器接周期为T=0.02s的低压交流电源。他经过测量和计算得到打点计时器打下B、C、D、E、F各点时小车的瞬时速度,记录在下面的表格中。
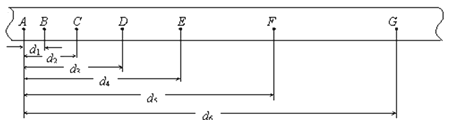
对应点 | B | C | D | E | F |
速度/ms-1 | 0.122 | 0.164 | 0.205 | 0.250 | 0.289 |
① 计算打点计时器打下F点时小车的瞬时速度的公式为 vF= ;
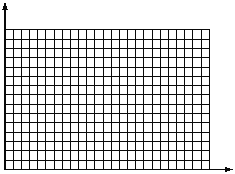
② 根据上面得到的数据,以A点对应的时刻为t=0时刻,在坐标纸上作出小车的速度随时间变化的v-t图线;
③由v-t图线求得小车的加速度a = m/s2(结果保留两位有效数字)。