题目内容
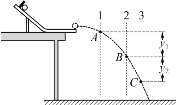
【题目】某实验小组设计了如图所示的实验装置来测量物块与斜面间的动摩擦因数，物块上方固定一个遮光条，并在斜面上靠近底端位置安装一个光电门，光电门连接数字计时器。
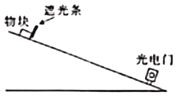
(1)若用毫米刻度尺测得遮光条的宽度为d，用数字计时器测得遮光条通过光电门的时间为t，则物块通过光电门时的速度大小为_____（用对应物理量的符号表示）；
(2)用量角器测出斜面的倾角θ；
(3)使物块分别从斜面上不同高度处无初速释放测出物块释放的初始位置到光电门的距离L1、L2、L3…，读出物块上遮光条每次通过光电门的时间t，计算出物块上遮光条每次通过光电门的速度v1、v2、v3…．若为了更直观地看出L和v的变化关系，则应该作出的图象是_____（填选项前的字母）
A．L﹣v图象
B．L﹣
图象
C．L﹣v2图象
D．L﹣
与图象
(4)若根据(3)正确选择的图象得出图线的斜率为k，重力加速度大小为g，则物块和斜面间的动摩擦因数为_____。
【答案】
C tanθ﹣
【解析】
(1)[1]若用毫米刻度尺测得遮光条的宽度为d，用数字计时器测得遮光条通过光电门的时间为t，则物块通过光电门时的速度大小为
v＝
(3)[2]由运动学公式可知
v2＝2aL
则为了更直观地看出L和v的变化关系，下面应该做出L﹣v2图象，故C正确，ABD错误；
故选C；
(4)[3]对物块进行受力分析，根据牛顿第二定律得
mgsinθ﹣μmgcosθ＝ma
解得
a＝gsinθ﹣μgcosθ
L﹣v2图象得出图线的斜率为k，所以
k＝
重力加速度大小为g，解得
μ＝tanθ﹣
练习册系列答案
相关题目
