题目内容
 一根弹性绳沿x轴方向放置,在原点O,用手握住绳的左端使其沿y轴方向做周期为1s的简谐运动,于是在绳上形成一列简谐波,如图所示,从波传到平衡位置在x=1m处的M质点时开始计时,求:
一根弹性绳沿x轴方向放置,在原点O,用手握住绳的左端使其沿y轴方向做周期为1s的简谐运动,于是在绳上形成一列简谐波,如图所示,从波传到平衡位置在x=1m处的M质点时开始计时,求:(1)从计时开始,经过多长时间,平衡位置在x=4.5m处的N质点开始振动
(1)从计时开始,经过多长时间,N质点恰好第一次沿y轴正向通过平衡位置?
(2)2.875s时,N点的位移?
分析:(1)根据图象读出波长,由波长与波速的关系,即可求解;
(2)先求出波传播到N质点的时间,再求出第一次沿y轴正向通过平衡位置的时间,然后两者之和,即可求解;
(3)根据时间确定是周期的多少倍,然后由分数部分,结合质点的振动方程,来确定N点的位移.
(2)先求出波传播到N质点的时间,再求出第一次沿y轴正向通过平衡位置的时间,然后两者之和,即可求解;
(3)根据时间确定是周期的多少倍,然后由分数部分,结合质点的振动方程,来确定N点的位移.
解答:解:(1)由图可知,波长λ=2m;
根据波速与波长的关系,则有:v=
=2m/s
平衡位置在x=4.5m处的N质点开始振动,波要传播3.5m;
则所用时间为:t1=
=
s=1.75s
(2)波要传播到N质点,传播距离为3.5m,;
所用时间为:t2=
s=1.75s
再经过半个周期恰好第一次沿y轴正向通过平衡位置,因此经过的时间为:t=t2+
=1.75s+0.5s=2.25s
(3)当时间为t3=2.875-2.25=0.625s
则有,0.625s=
T
由y=Asin
π=8×
m=4
m
答:(1)从计时开始,经过1.75s时间,平衡位置在x=4.5m处的N质点开始振动;
(2)从计时开始,经过2.25s时间,N质点恰好第一次沿y轴正向通过平衡位置;
(3)2.875s时,N点的位移为4
m.
根据波速与波长的关系,则有:v=
| λ |
| T |
平衡位置在x=4.5m处的N质点开始振动,波要传播3.5m;
则所用时间为:t1=
| s |
| v |
| 3.5 |
| 2 |
(2)波要传播到N质点,传播距离为3.5m,;
所用时间为:t2=
| 3.5 |
| 2 |
再经过半个周期恰好第一次沿y轴正向通过平衡位置,因此经过的时间为:t=t2+
| T |
| 2 |
(3)当时间为t3=2.875-2.25=0.625s
则有,0.625s=
| 5 |
| 8 |
由y=Asin
| 5 |
| 4 |
| ||
| 2 |
| 2 |
答:(1)从计时开始,经过1.75s时间,平衡位置在x=4.5m处的N质点开始振动;
(2)从计时开始,经过2.25s时间,N质点恰好第一次沿y轴正向通过平衡位置;
(3)2.875s时,N点的位移为4
| 2 |
点评:考查波长、波速与周期的关系,注意波传播到N质点时,质点沿y轴负方向传播,这是解题的关键.同时掌握由时刻来确定质点的位置的方法.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 一根弹性绳沿x轴方向放置,左端在原点O,用手握住绳的左端使其沿y轴方向做周期为1s的简谐运动,于是在绳上形成一列简谐波.求:
一根弹性绳沿x轴方向放置,左端在原点O,用手握住绳的左端使其沿y轴方向做周期为1s的简谐运动,于是在绳上形成一列简谐波.求: (2013?河南模拟)一根弹性绳沿x轴方向放置,左端在原点O处,用手握住绳的左端使其沿y轴方向做简谐运动,在绳上形成一简谐波,绳上质点N的平衡位置为x=5m,从绳左端开始振动计时,经过0.5s振动传播到质点M时的波形如图所示,求:
(2013?河南模拟)一根弹性绳沿x轴方向放置,左端在原点O处,用手握住绳的左端使其沿y轴方向做简谐运动,在绳上形成一简谐波,绳上质点N的平衡位置为x=5m,从绳左端开始振动计时,经过0.5s振动传播到质点M时的波形如图所示,求: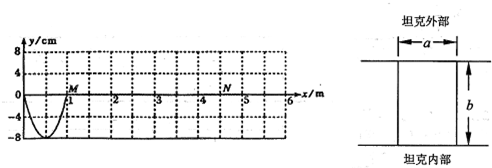
 一根弹性绳沿x轴方向放置,左端在原点O处,用手握住绳的左端使其沿y轴方向做周期为1s的简谐运动,于是在绳上形成一简谐波,绳上质点N的平衡位置为x=5m,振动传播到质点M时的波形如图所示,求:
一根弹性绳沿x轴方向放置,左端在原点O处,用手握住绳的左端使其沿y轴方向做周期为1s的简谐运动,于是在绳上形成一简谐波,绳上质点N的平衡位置为x=5m,振动传播到质点M时的波形如图所示,求: