题目内容
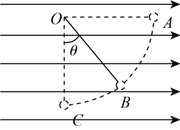
【题目】如图所示,匀强电场仅分布在第一、二象限,方向沿y轴负方向,一不计重力的带正电粒子比荷为5.0×109C/kg,以v0=3.0×105m/s从第二象限的M(-12cm,8cm)点,沿x轴正方向射入匀强电场中,粒子经过电场偏转后到达坐标原点O。求:
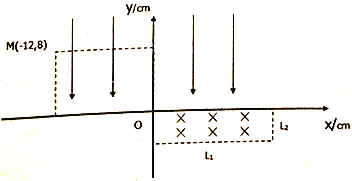
(1)该电场强度大小?粒子到达O点时的速度大小和方向?
(2)若第四象限存在一个以x、y轴为边界的矩形匀强磁场,已知L1=15cm、L2=4cm,磁场方向垂直纸面向里,若要带电粒子能返回x轴,磁感应强度B需要满足什么条件?
(3)若该粒子能回到x轴,求其返回x轴时的最大横坐标为多少?(结果可用根式表示)
【答案】(1) 5.0×105m/s(2) B≥1.0×10-3T(3)![]()
【解析】(1)粒子在第二象限偏转,x1=0.12m,y1=0.08m,由牛顿第二定律
qE=ma
x1=v0t1
y1=![]() at12
at12
由-得,E=200v/m
带电粒子从O点进入磁场时的速度大小为v,方向与x轴夹角为θ
tanθ=![]() 得θ=53o
得θ=53o
v=![]() =5.0×105m/s
=5.0×105m/s
(2)带电粒子m恰返回x轴,由几何关系
cosθ=![]() ,得R=0.1m
,得R=0.1m
设磁感应强度的最小值为B0,洛伦兹力提供向心力
qvB0=m![]() ,得B0=1.0×10-3T
,得B0=1.0×10-3T
即B≥1.0×10-3T,带电粒子m能返回x轴
(3)当B取B0时,粒子返回x轴时横坐标最大
设离开磁场时,速度与x轴正向夹角为α,则由几何关系
L1-Rsinθ=Rsinα,得sinα=0.7,
则![]() ,
,![]() ……………2分
……………2分
离开磁场后,粒子做匀速直线运动,沿x轴运动x2
则Rcosα-Rcosθ=x2tanα
得![]()
故粒子返回x轴时的最大横坐标![]()

练习册系列答案
相关题目