题目内容
【题目】如图所示，在真空中有一个半径为R，质量均匀分布的玻璃球，一细激光束在真空中沿直线BC传播，并于玻璃球表面的C点经折射后进入玻璃球，在玻璃球表面上的另外一点D又折射后进人真空，半径CO与DO的夹角为120°，玻璃球对该激光的折射率为
，光在真空中传播的速度为c，则：
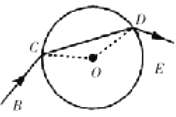
①此激光束在玻璃球中传播的时间是多少；
②入射角i是多少.
【答案】①
②i=60°
【解析】试题分析：（i）根据几何关系求出光在束在玻璃砖内传播的距离，由
求出光在玻璃砖传播的速度，即可求出传播的时间．（ii）由几何知识求出光线在C点的折射角r，由折射定律求出入射角i．
（i）根据题意作出大致光路图，如图所示：
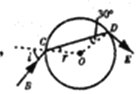
根据
，得
由几何关系可知，光在玻璃球中传播的距离为
则传播时间
（ii）由几何知识知，光线在C点的折射角
根据折射定律
，
解得
故入射角
练习册系列答案
手拉手全优练考卷系列答案
相关题目
