题目内容
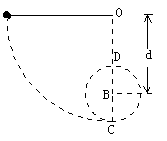
小球A用不可伸长的轻绳悬于O点，在O点的正下方有一固定的钉子B，OB=d，初始时小球A与O同水平面无初速释放，绳长为l，为使球能绕B点做圆周运动，试求d的取值范围？
球能绕B点做圆周运动，在D点根据向心力公式有：
mg+F=m
当F=0时，速度取最小值
所以v≥
=
对小球从最高点运动到D点的过程中运用动能定理得：
mv2-0=mg(2d-l)
解得：v=
所以
≥
解得：d≥
l
由题意得d＜l
所以有：l＞d≥
l
答：d的取值范围为：l＞d≥
l
mg+F=m
| v2 |
| r |
当F=0时，速度取最小值
所以v≥
| gr |
| g(l-d) |
对小球从最高点运动到D点的过程中运用动能定理得：
| 1 |
| 2 |
解得：v=
| 2g(2d-l) |
所以
| 2g(2d-l) |
| g(l-d) |
解得：d≥
| 3 |
| 5 |
由题意得d＜l
所以有：l＞d≥
| 3 |
| 5 |
答：d的取值范围为：l＞d≥
| 3 |
| 5 |
练习册系列答案
孟建平错题本系列答案
超能学典应用题题卡系列答案
相关题目
小球A用不可伸长的轻绳悬于O点，在O点的正下方有一固定的钉子B，OB=d，初始时小球A与O同水平面无初速释放，绳长为l，为使球能绕B点做圆周运动，试求d的取值范围？
