题目内容
2.在用单摆测重力加速度的实验中:(1)实验时必须控制摆角很小,并且要让单摆在同一竖直平面内摆动.
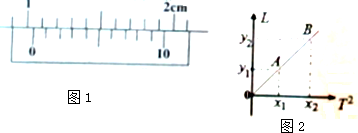
(2)用游标卡尺测定摆球的直径,测量结果如图1所示,则摆球的直径为10.4mm.
(3)某同学测出不同摆长时对应的周期T,作出L-T2图线如图2所示,利用图线上任意两点A、B的坐标(x1,y1)、(x2,、y2),可求得g=$\frac{4{π}^{2}({y}_{2}-{y}_{1})}{{x}_{2}-{x}_{1}}$.
(4)某同学测单摆振动周期时,由于计数错误将29次全振动的时间记为了30次,而其他测量和计算均无误,由此造成的结果是g的测量值大于(选填“大于”或“小于”)真实值.
分析 (1)单摆应在同一竖直平面内振动,不能绕单摆转圈,成为圆锥摆.
(2)游标卡尺主尺与游标尺示数之和是游标卡尺的示数.
(3)由单摆周期公式求出图象的函数表达式,然后根据图示图象求出重力加速度.
(4)根据单摆周期工作求出重力加速度的表达式,然后分析实验误差.
解答 解:(1)实验时必须控制摆角很小,并且要让单摆在同一竖直平面内摆动.
(2)由图示游标卡尺可知,其示数为10mm+4×0.1mm=10.4mm.
(3)由单摆周期公式:T=2π$\sqrt{\frac{L}{g}}$可知,L=$\frac{g}{4{π}^{2}}$T2,L-T2图象的斜率:k=$\frac{g}{4{π}^{2}}$=$\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}$,重力加速度:g=$\frac{4{π}^{2}({y}_{2}-{y}_{1})}{{x}_{2}-{x}_{1}}$;
(4)由单摆周期公式:T=2π$\sqrt{\frac{L}{g}}$可知:g=$\frac{4{π}^{2}L}{{T}^{2}}$,将29次全振动的时间记为了30次,所测周期T偏小,重力加速度g偏大;
故答案为:(1)同一竖直;(2)10.4;(3)$\frac{4{π}^{2}({y}_{2}-{y}_{1})}{{x}_{2}-{x}_{1}}$;(4)大于.
点评 本题考查了应用单摆测重力加速度实验,要知道实验的注意事项、掌握游标卡尺的读数方法,应用单摆周期公式即可解题;游标卡尺主尺与游标尺示数之和是游标卡尺的示数,游标卡尺不需要估读.

练习册系列答案
相关题目
12.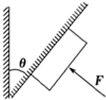 如图所示,倾斜天花板平面与竖直平面夹角为θ,推力F垂直天花板平面作用在质量为m的木块上,使其处于静止状态,则下列说法正确的是( )
如图所示,倾斜天花板平面与竖直平面夹角为θ,推力F垂直天花板平面作用在质量为m的木块上,使其处于静止状态,则下列说法正确的是( )
 如图所示,倾斜天花板平面与竖直平面夹角为θ,推力F垂直天花板平面作用在质量为m的木块上,使其处于静止状态,则下列说法正确的是( )
如图所示,倾斜天花板平面与竖直平面夹角为θ,推力F垂直天花板平面作用在质量为m的木块上,使其处于静止状态,则下列说法正确的是( )| A. | 木块可能受三个力作用 | |
| B. | 天花板对木块的弹力等于F-mgsin θ | |
| C. | 木块受的静摩擦力可能等于0 | |
| D. | 木块受的静摩擦力等于mgsin θ |
10. 如图所示,变压器的原、副线圈的匝数比一定,原线圈的电压为U1时,副线圈的输出电压为U2,L1、L2、L3是三只完全相同的电灯.开始时,开关S是断开的,现将S闭合,则( )
如图所示,变压器的原、副线圈的匝数比一定,原线圈的电压为U1时,副线圈的输出电压为U2,L1、L2、L3是三只完全相同的电灯.开始时,开关S是断开的,现将S闭合,则( )
 如图所示,变压器的原、副线圈的匝数比一定,原线圈的电压为U1时,副线圈的输出电压为U2,L1、L2、L3是三只完全相同的电灯.开始时,开关S是断开的,现将S闭合,则( )
如图所示,变压器的原、副线圈的匝数比一定,原线圈的电压为U1时,副线圈的输出电压为U2,L1、L2、L3是三只完全相同的电灯.开始时,开关S是断开的,现将S闭合,则( )| A. | L1变亮,L2变暗 | B. | L1变暗,L2变亮 | ||
| C. | U1、U2均不变 | D. | 原线圈中的电流变大 |
17. 一列简谐横波沿x轴负向传波,t时刻波的图象如图所示,P是介质中的一个质点,已知P质点在1s时间内运动的路程为16cm,则下列说法正确的是( )
一列简谐横波沿x轴负向传波,t时刻波的图象如图所示,P是介质中的一个质点,已知P质点在1s时间内运动的路程为16cm,则下列说法正确的是( )
 一列简谐横波沿x轴负向传波,t时刻波的图象如图所示,P是介质中的一个质点,已知P质点在1s时间内运动的路程为16cm,则下列说法正确的是( )
一列简谐横波沿x轴负向传波,t时刻波的图象如图所示,P是介质中的一个质点,已知P质点在1s时间内运动的路程为16cm,则下列说法正确的是( )| A. | 该波的波长为2m | B. | 该波的波速为1m/s | ||
| C. | t时刻P质点的速度方向向左 | D. | t时刻P质点的速度方向向下 |
7. 如图所示,质量为m的小球,用长为L的细线悬挂在O点,在O点正下方$\frac{L}{2}$处有一光滑的钉子P,把小球拉到与钉子等高的位置A,悬线被钉子挡住.让小球在位置A由静止释放,当小球第一次经过最低点时( )
如图所示,质量为m的小球,用长为L的细线悬挂在O点,在O点正下方$\frac{L}{2}$处有一光滑的钉子P,把小球拉到与钉子等高的位置A,悬线被钉子挡住.让小球在位置A由静止释放,当小球第一次经过最低点时( )
 如图所示,质量为m的小球,用长为L的细线悬挂在O点,在O点正下方$\frac{L}{2}$处有一光滑的钉子P,把小球拉到与钉子等高的位置A,悬线被钉子挡住.让小球在位置A由静止释放,当小球第一次经过最低点时( )
如图所示,质量为m的小球,用长为L的细线悬挂在O点,在O点正下方$\frac{L}{2}$处有一光滑的钉子P,把小球拉到与钉子等高的位置A,悬线被钉子挡住.让小球在位置A由静止释放,当小球第一次经过最低点时( )| A. | 小球的线速度突然增大 | B. | 小球的角速度突然减小 | ||
| C. | 悬线上的拉力突然减小 | D. | 小球的向心加速度突然增大 |
11. 如图,一理想变压器原、副线圈匝数比为4:1,原线圈与一可变电阻串联后,接入一正弦交流电源;副线圈电路中固定电阻的阻值为R0,负载电阻的阻值R=11R0,V是理想电压表;现将负载电阻的阻值减小为R=5R0,保持变压器输入电流不变,此时电压表读数为5V,则( )
如图,一理想变压器原、副线圈匝数比为4:1,原线圈与一可变电阻串联后,接入一正弦交流电源;副线圈电路中固定电阻的阻值为R0,负载电阻的阻值R=11R0,V是理想电压表;现将负载电阻的阻值减小为R=5R0,保持变压器输入电流不变,此时电压表读数为5V,则( )
 如图,一理想变压器原、副线圈匝数比为4:1,原线圈与一可变电阻串联后,接入一正弦交流电源;副线圈电路中固定电阻的阻值为R0,负载电阻的阻值R=11R0,V是理想电压表;现将负载电阻的阻值减小为R=5R0,保持变压器输入电流不变,此时电压表读数为5V,则( )
如图,一理想变压器原、副线圈匝数比为4:1,原线圈与一可变电阻串联后,接入一正弦交流电源;副线圈电路中固定电阻的阻值为R0,负载电阻的阻值R=11R0,V是理想电压表;现将负载电阻的阻值减小为R=5R0,保持变压器输入电流不变,此时电压表读数为5V,则( )| A. | 此时原线圈两端电压的有效值为24V | |
| B. | 此时原线圈两端电压的有效值为34V | |
| C. | 原来电压表的示数为11V | |
| D. | 原来电压表的示数为16V |
 如图所示为游乐场中深受大家喜爱的“激流勇进”的娱乐项目,人坐在船中,随着提升机达到高处,再沿着倾斜水槽快速滑下,劈波斩浪的刹那给人惊险刺激的感受.设乘客与船的总质量为100kg,倾斜水槽的坡度为30°.若乘客与船从槽顶部由静止开始滑行36m到达倾斜水槽底部,速度大小为12$\sqrt{2}$m/s,取g=10m/s2.求:
如图所示为游乐场中深受大家喜爱的“激流勇进”的娱乐项目,人坐在船中,随着提升机达到高处,再沿着倾斜水槽快速滑下,劈波斩浪的刹那给人惊险刺激的感受.设乘客与船的总质量为100kg,倾斜水槽的坡度为30°.若乘客与船从槽顶部由静止开始滑行36m到达倾斜水槽底部,速度大小为12$\sqrt{2}$m/s,取g=10m/s2.求: 如图所示,在同一竖直平面内,一轻质弹簧下端固定在位置E,上端恰好与水平线CD齐平,静止在倾角为θ=53°的光滑斜面上.一长为L=1.8m的轻质细绳一端固定在O点上,另一端系一质量为m=1kg的小球,将细绳拉至水平,使小球从位置A由静止释放,小球到达最低点B时,细绳刚好被拉断.之后小球恰好沿着斜面方向撞上弹簧上端并将弹簧压缩,最大压缩量为x=0.5m.取g=10m/s2,sin53°=0.8,cos53°=0.6.求:
如图所示,在同一竖直平面内,一轻质弹簧下端固定在位置E,上端恰好与水平线CD齐平,静止在倾角为θ=53°的光滑斜面上.一长为L=1.8m的轻质细绳一端固定在O点上,另一端系一质量为m=1kg的小球,将细绳拉至水平,使小球从位置A由静止释放,小球到达最低点B时,细绳刚好被拉断.之后小球恰好沿着斜面方向撞上弹簧上端并将弹簧压缩,最大压缩量为x=0.5m.取g=10m/s2,sin53°=0.8,cos53°=0.6.求: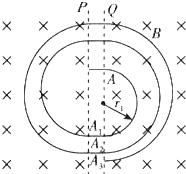 如图所示,相距为d的狭缝P、Q间存在着方向始终与P、Q平面垂直、电场强度大小为E的匀强电场,且电场的方向按一定规律分时段变化.狭缝两侧均有磁感强度大小为B、方向垂直纸面向里的匀强磁场,且磁场区域足够大.某时刻从P平面处由静止释放一个质量为m、带电荷为q的带负电的粒子(不计重力),粒子被加速后由A点进入Q平面右侧磁场区,以半径r1做圆运动,此时电场的方向已经反向,当粒子由A1点自右向左通过Q平面后,使粒子再次被加速进入P平面左侧磁场区做圆运动,此时电场又已经反向,粒子经半个圆周后通过P平面进入PQ狭缝又被加速,….以后粒子每次通过PQ间都被加速.设粒子自右向左穿过Q平面的位置依次分别是A1、A2、A3、…An…,求:
如图所示,相距为d的狭缝P、Q间存在着方向始终与P、Q平面垂直、电场强度大小为E的匀强电场,且电场的方向按一定规律分时段变化.狭缝两侧均有磁感强度大小为B、方向垂直纸面向里的匀强磁场,且磁场区域足够大.某时刻从P平面处由静止释放一个质量为m、带电荷为q的带负电的粒子(不计重力),粒子被加速后由A点进入Q平面右侧磁场区,以半径r1做圆运动,此时电场的方向已经反向,当粒子由A1点自右向左通过Q平面后,使粒子再次被加速进入P平面左侧磁场区做圆运动,此时电场又已经反向,粒子经半个圆周后通过P平面进入PQ狭缝又被加速,….以后粒子每次通过PQ间都被加速.设粒子自右向左穿过Q平面的位置依次分别是A1、A2、A3、…An…,求: