题目内容
一人用一根长L=1m，最大只能承受T=46N拉力的轻绳子，拴着一个质量m=1kg的小球（不考虑其大小），在竖直平面内作圆周运动，已知圆心O离地高H=21m，如图所示，若小球运动到达最低点时绳刚好被球拉断，（g=10m/s2）求：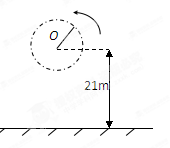
（1）小球到达最低点的速度大小是多少?
（2）小球落地点到O点的水平距离是多少?
（1）6m/s（2）12m
解析试题分析：（1）在最低点，小球做圆周运动的向心力是拉力和重力的合力，故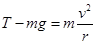
绳子要断开，拉力达到最大值46N，带入数据得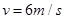
（2）因为在最低点的速度是水平的，所以断开后，小球做平抛运动，抛出点离地面的高度为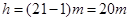
由平抛运动规律得，竖直方向上
，水平方向
带入数据得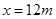
。
考点：考查了圆周运动，平抛运动规律的应用
练习册系列答案
相关题目
平抛运动可以分解为水平和竖直两个方向的直线运动，在同一坐标系中作出这两个分运动的v-t图像，如图所示，若平抛运动的时间大于2t1, g=10m/s2, 则下列说法中正确的是: 
| A．图线1表示竖直分运动的v－t图线 |
| B．图线2表示水平分运动的v－t图线 |
| C．t1时间内物体速度的变化量大小为20t1(m/s),方向与水平方向成450 |
| D．t1时刻的速度方向与初速度方向夹角为45° |
的速度水平飞出（g取10 m/s2）．求：
