题目内容
11. 如图所示,倾斜的直杆AB 与水平面成α并角固定,在杆上套一质量为m的小滑块,杆底端B 点处有一弹性挡板,杆与板面垂直,滑块与挡板碰撞后将原速率返回.现将滑块拉到A 点由静止释放,小滑块与挡板第一次碰撞后恰好能上升到AB 的中点,设重力加速度为g,由此不能确定的是( )
如图所示,倾斜的直杆AB 与水平面成α并角固定,在杆上套一质量为m的小滑块,杆底端B 点处有一弹性挡板,杆与板面垂直,滑块与挡板碰撞后将原速率返回.现将滑块拉到A 点由静止释放,小滑块与挡板第一次碰撞后恰好能上升到AB 的中点,设重力加速度为g,由此不能确定的是( )| A. | 滑块下滑和上滑过程加速度的大小a1、a2 | |
| B. | 滑块最终所处的位置 | |
| C. | 滑块与杆之间动摩擦因数μ | |
| D. | 滑块第k 次与挡板碰撞后速度vk |
分析 滑块运动分两个阶段,匀加速下滑和匀减速上滑,利用牛顿第二定律求出两端加速度,利用运动学公式求解.
解答 解:A、设下滑位移为L,到达底端速度为v
由公式v2=2ax得:
下滑过程:v2=2a下L ①
上滑过程:v2=2a上$\frac{L}{2}$=a上L ②
由牛顿第二定律得:
下滑加速度为:a下=$\frac{mgsinα-f}{m}$ ③
上滑加速度为:a上=$\frac{mgsinα+f}{m}$ ④
①②③④联立得:a下=$\frac{2gsinα}{3}$,a上=$\frac{4gsinα}{3}$,故A正确;
B、f=$\frac{1}{3}$mgsinα,又f=μFN=μmgcosα两式联立得:μ=$\frac{1}{3}$,
因为滑杆粗糙,所以最终滑块停在底端,故BC正确;
D、因为不知道最初滑块下滑的位移,所以无法求出速度,故D错误;
本题选不能确定的,故选:D
点评 解决本题的关键是上滑和下滑时摩擦力方向不同,所以加速度不同,另外抓住连接两段的桥梁是碰撞前后速度大小相等.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
17.下列说法正确的是( )
| A. | 牛顿发现了万有引力定律并测定了引力常量 | |
| B. | 伽利略发现了行星运动三定律 | |
| C. | 安培发现了电流的磁效应 | |
| D. | 法拉第最先在物理学中引入电场和电场线的概念 |
18.Bungee(蹦极)是一种新兴的体育活动,蹦跃者站在约40米以上(相当于10层楼高)高度的桥梁、塔顶、高楼、吊车甚至热气球上,把一端固定的一根长长的橡皮条绑在踝关节处,然后两臂伸开,双腿并拢,头朝下跳下去.绑在跳跃者踝部的橡皮条很长,足以使跳跃者在空中享受几秒钟的“自由落体”.当人体落到离地面一定距离时,橡皮绳被拉开、绷紧,阻止人体继续下落,当人到达最低点时,橡皮绳再次弹起,人被拉起,随后又落下,如此反复,但由于空气阻力的原因,使弹起的高度会逐渐减小,直到静止,这就是蹦极的全过程.根据以上的叙述,忽略空气阻力的影响,对第一次下落过程中下列说法正确的是( )
| A. | 当橡皮绳达到原长后人开始做减速运动 | |
| B. | 整个下落过程中人的机械能守恒 | |
| C. | 当橡皮绳的弹力刚好等于人的重力时人的加速度最大 | |
| D. | 当人达到最低点时加速度数值最大,且一定大于重力加速度g的值 |
15. 如图所示,在超市中,小张沿水平方向推着质量为m的购物车乘着沿自动扶梯方向加速度为a匀加速上升的自动扶梯上楼.假设小张、购物车、自动扶梯间保持相对静止,自动扶梯的倾角为θ,小张的质量为M,小张与扶梯间的摩擦因数为μ,小车与扶梯间的摩擦忽略不计.则( )
如图所示,在超市中,小张沿水平方向推着质量为m的购物车乘着沿自动扶梯方向加速度为a匀加速上升的自动扶梯上楼.假设小张、购物车、自动扶梯间保持相对静止,自动扶梯的倾角为θ,小张的质量为M,小张与扶梯间的摩擦因数为μ,小车与扶梯间的摩擦忽略不计.则( )
 如图所示,在超市中,小张沿水平方向推着质量为m的购物车乘着沿自动扶梯方向加速度为a匀加速上升的自动扶梯上楼.假设小张、购物车、自动扶梯间保持相对静止,自动扶梯的倾角为θ,小张的质量为M,小张与扶梯间的摩擦因数为μ,小车与扶梯间的摩擦忽略不计.则( )
如图所示,在超市中,小张沿水平方向推着质量为m的购物车乘着沿自动扶梯方向加速度为a匀加速上升的自动扶梯上楼.假设小张、购物车、自动扶梯间保持相对静止,自动扶梯的倾角为θ,小张的质量为M,小张与扶梯间的摩擦因数为μ,小车与扶梯间的摩擦忽略不计.则( )| A. | 小张对扶梯的压力大小为Mgcosθ,方向垂直于斜面向下 | |
| B. | 小张对扶梯的摩擦力大小为(M+m)(gsin θ+a),方向沿斜面向下 | |
| C. | 扶梯对小张的摩擦力大小为μ(M+m)gcosθ,方向沿斜面向上 | |
| D. | 小张对车的推力和车对小张的弹力是一对平衡力,因为人和车处于平衡状态,所以两者大小相等 |
20.以下说法正确的是( )
| A. | 布朗运动是液体分子的运动,它说明了分子在永不停息地做无规则运动 | |
| B. | 密封在容积不变的容器内的气体,若温度升高,则气体分子对器壁单位面积上的平均作用力增大 | |
| C. | 某气体的摩尔质量为M、摩尔体积为V、密度为ρ,用NA表示阿伏伽德罗常数,每个气体分子的质量m0=$\frac{M}{{N}_{A}}$,每个气体分子的体积V0=$\frac{M}{ρ{N}_{A}}$ | |
| D. | 根据热力学第二定律可知,热量能够从高温物体传到低温物体,也可以从低温物体传到高温物体 | |
| E. | 液晶显示屏是应用液晶的光学各向异性制成的 |
1.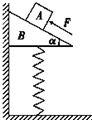 如图所示,物块A放在直角三角形斜面体B上面,B放在弹簧上面并紧挨着竖直墙壁,初始时A、B静止;现用力F沿斜面向上推A,但A、B仍未动.则施力F后,下列说法正确的是( )
如图所示,物块A放在直角三角形斜面体B上面,B放在弹簧上面并紧挨着竖直墙壁,初始时A、B静止;现用力F沿斜面向上推A,但A、B仍未动.则施力F后,下列说法正确的是( )
 如图所示,物块A放在直角三角形斜面体B上面,B放在弹簧上面并紧挨着竖直墙壁,初始时A、B静止;现用力F沿斜面向上推A,但A、B仍未动.则施力F后,下列说法正确的是( )
如图所示,物块A放在直角三角形斜面体B上面,B放在弹簧上面并紧挨着竖直墙壁,初始时A、B静止;现用力F沿斜面向上推A,但A、B仍未动.则施力F后,下列说法正确的是( )| A. | 弹簧弹力一定不变 | B. | B与墙面的弹力可能不变 | ||
| C. | B与墙之间一定有摩擦力 | D. | A、B之间的摩擦力一定变大 |
 如图竖直放置的两块足够长的平行金属板间有匀强电场,其场强为E,在该电场中,用丝线悬挂一个质量为m的带电小球,当丝线和竖直方向夹角θ=30°时,小球恰处于平衡状态,此时小球距右板的距离为d,求
如图竖直放置的两块足够长的平行金属板间有匀强电场,其场强为E,在该电场中,用丝线悬挂一个质量为m的带电小球,当丝线和竖直方向夹角θ=30°时,小球恰处于平衡状态,此时小球距右板的距离为d,求
 如图所示,物A重 GA=20N,物B重 GB=20N,A与水平桌面间的动摩擦因数μ=0.1,连接A、B间绳子与水平面夹角为53°,绳重、绳与定滑轮间的摩擦均不计.问水平拉力F应满足什么条件时才能使A处于静止状态?(可认为最大静摩擦力和滑动摩擦力大小相等) (g取10m/s2,sin53°=0.8,cos53°=0.6)
如图所示,物A重 GA=20N,物B重 GB=20N,A与水平桌面间的动摩擦因数μ=0.1,连接A、B间绳子与水平面夹角为53°,绳重、绳与定滑轮间的摩擦均不计.问水平拉力F应满足什么条件时才能使A处于静止状态?(可认为最大静摩擦力和滑动摩擦力大小相等) (g取10m/s2,sin53°=0.8,cos53°=0.6)