题目内容
4. 有一匀强电场,其场强为E=4×1015v/m,方向竖直向下.把一个半径为r=0.1米的光滑绝缘环,竖直置于电场中,环面平行于电场线,环的顶点A穿有一个质量为m=0.01kg、电量为q=-5×10-17c的空心小球,如图所示.当小球从A点给它一个初速度v0开始刚好做圆周运动,则小球回到A点时对环的压力多大?v0多大?
有一匀强电场,其场强为E=4×1015v/m,方向竖直向下.把一个半径为r=0.1米的光滑绝缘环,竖直置于电场中,环面平行于电场线,环的顶点A穿有一个质量为m=0.01kg、电量为q=-5×10-17c的空心小球,如图所示.当小球从A点给它一个初速度v0开始刚好做圆周运动,则小球回到A点时对环的压力多大?v0多大?
分析 先分别求出电场力和重力,比较它们的大小.电场力大于重力,合力方向上,要使小球刚好做圆周运动,在B点时,由电场力与重力的合力提供向心力,求出B点的临界速度,再由动能定理求v0.由牛顿运动定律求小球回到A点时对环的压力.
解答 解:小球所受的电场力大小 F电=qE=0.2N,方向竖直向上;重力 G=mg=0.1N
因F电>G,故B点是“等效最高点”.要使小球刚好做圆周运动,在B点时,由电场力与重力的合力提供向心力,则在B点有:F电-G=m$\frac{{v}_{B}^{2}}{r}$
从B到A,由动能定理得:(F电-G)•2r=$\frac{1}{2}m{v}_{0}^{2}-\frac{1}{2}m{v}_{B}^{2}$
解得:v0=2$\sqrt{3}$m/s
在A点,由牛顿第二定律得:N-(F电-G)=m$\frac{{v}_{0}^{2}}{r}$
可得 N=1.3N
由牛顿第三定律得,小球回到A点时对环的压力大小为1.3N,方向向上.
答:小球回到A点时对环的压力大小为1.3N,方向向上.v0为2$\sqrt{3}$m/s.
点评 本题考查了牛顿第二定律和动能定理的基本运用,关键要找到物理最高点,知道向心力的来源,结合牛顿第二定律和第三定律进行求解.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
15. 如图所示,实线表示匀强电场的电场线.一个带正电荷的粒子以某-速度射入匀强电场,只在电场力作用下,运动的轨迹如图中的虚线所示,a、b为轨迹上的两点.若a点电势为φa,b点电势为φb,则( )
如图所示,实线表示匀强电场的电场线.一个带正电荷的粒子以某-速度射入匀强电场,只在电场力作用下,运动的轨迹如图中的虚线所示,a、b为轨迹上的两点.若a点电势为φa,b点电势为φb,则( )
 如图所示,实线表示匀强电场的电场线.一个带正电荷的粒子以某-速度射入匀强电场,只在电场力作用下,运动的轨迹如图中的虚线所示,a、b为轨迹上的两点.若a点电势为φa,b点电势为φb,则( )
如图所示,实线表示匀强电场的电场线.一个带正电荷的粒子以某-速度射入匀强电场,只在电场力作用下,运动的轨迹如图中的虚线所示,a、b为轨迹上的两点.若a点电势为φa,b点电势为φb,则( )| A. | 场强方向一定向左,且电势φa<φb | B. | 场强方向一定向右,且电势φa>φb | ||
| C. | 该粒子的电势能将不断减少 | D. | 该粒子做匀变速运动 |
12. 用同一光电管研究a、b两种单色光产生的光电效应,得到光电流I与光电管两极间所加电压U的关系如图,则这两种光( )
用同一光电管研究a、b两种单色光产生的光电效应,得到光电流I与光电管两极间所加电压U的关系如图,则这两种光( )
 用同一光电管研究a、b两种单色光产生的光电效应,得到光电流I与光电管两极间所加电压U的关系如图,则这两种光( )
用同一光电管研究a、b两种单色光产生的光电效应,得到光电流I与光电管两极间所加电压U的关系如图,则这两种光( )| A. | 照射该光电管时b光使其逸出的光电子最大初动能大 | |
| B. | 从同种玻璃射入空气发生全反射时,b光的临界角大 | |
| C. | 通过同一装置发生双缝干涉,b光的相邻条纹间距大 | |
| D. | 根据玻尔理论可知,产生b光时原子的能级差大 |
19.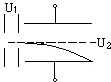 如图所示,电子经加速电场(电压为U1)后进入偏转电场(电压为U2),然后飞出偏转电场,要使电子飞不出偏转电场可采取的措施有( )
如图所示,电子经加速电场(电压为U1)后进入偏转电场(电压为U2),然后飞出偏转电场,要使电子飞不出偏转电场可采取的措施有( )
 如图所示,电子经加速电场(电压为U1)后进入偏转电场(电压为U2),然后飞出偏转电场,要使电子飞不出偏转电场可采取的措施有( )
如图所示,电子经加速电场(电压为U1)后进入偏转电场(电压为U2),然后飞出偏转电场,要使电子飞不出偏转电场可采取的措施有( )| A. | 增大U1 | B. | 减小U1 | C. | 减小U2 | D. | 以上都错 |
9. 如图所示,一块铜板放在磁场中,板面与磁场方向垂直,板内通有如图所示方向的电流,a、b是铜板左、右边缘的两点,则下列判断正确的是( )
如图所示,一块铜板放在磁场中,板面与磁场方向垂直,板内通有如图所示方向的电流,a、b是铜板左、右边缘的两点,则下列判断正确的是( )
 如图所示,一块铜板放在磁场中,板面与磁场方向垂直,板内通有如图所示方向的电流,a、b是铜板左、右边缘的两点,则下列判断正确的是( )
如图所示,一块铜板放在磁场中,板面与磁场方向垂直,板内通有如图所示方向的电流,a、b是铜板左、右边缘的两点,则下列判断正确的是( )| A. | 电势Ua>Ub | |
| B. | 电势Ub>Ua | |
| C. | 仅电流增大时,|Ua-Ub|增大 | |
| D. | 其它条件不变,将铜板改为NaCl的水溶液时,电势Ub>Ua |
16.甲、乙、丙三人各乘一艘飞艇,甲看到楼房匀速上升,乙看到甲艇匀速上升,丙看到乙艇匀速下降,甲看到丙艇匀速上升,则甲、乙、丙艇相对于地球的运动情况可能是( )
| A. | 甲和乙匀速下降,且 v 乙>v 甲,丙静止 | |
| B. | 甲和乙匀速下降,且 v 乙>v 甲,丙匀速上升 | |
| C. | 甲和乙匀速下降,且 v 乙>v 甲,丙匀速下降 | |
| D. | 甲匀速下降,乙匀速上升,丙静止不动 |
14.一列简谐横波沿x轴正方向传播,波速为v,位于x=0处的波源从平衡位置开始沿y轴正方向Z简谐运动,振动周期为T,质点P在x=2.5vT处,下列说法正确的是( )
| A. | 质点P振动周期为T,速度的最大值为v? | |
| B. | 若某时刻质点P的速度方向沿y轴负方向,则该时刻波源速度方向沿y轴正方向? | |
| C. | 质点P开始振动的方向沿y轴正方向? | |
| D. | 若某时刻波源在波峰,则质点P-定在波谷? | |
| E. | 若某时刻波源在波谷,则质点P-定在波谷 |


 如图所示,在竖直平面内的平面直角坐标系xoy中,x轴上方有水平向右的匀强电场,有一质量为m,电荷量为-q(-q<0)的带电绝缘小球,从y轴上的P(0,L)点由静止开始释放,运动至x轴上的A(-L,0)点时,恰好无碰撞地沿切线方向进入在x轴下方竖直放置的四分之三圆弧形光滑绝缘细管.细管的圆心O1位于y轴上,交y轴于点B,交x轴于A点和C(L,0)点.该细管固定且紧贴x轴,内径略大于小球外径.小球直径远小于细管半径,不计一切阻力,重力加速度为g.求:
如图所示,在竖直平面内的平面直角坐标系xoy中,x轴上方有水平向右的匀强电场,有一质量为m,电荷量为-q(-q<0)的带电绝缘小球,从y轴上的P(0,L)点由静止开始释放,运动至x轴上的A(-L,0)点时,恰好无碰撞地沿切线方向进入在x轴下方竖直放置的四分之三圆弧形光滑绝缘细管.细管的圆心O1位于y轴上,交y轴于点B,交x轴于A点和C(L,0)点.该细管固定且紧贴x轴,内径略大于小球外径.小球直径远小于细管半径,不计一切阻力,重力加速度为g.求: