题目内容
7. 在如图所示的倾角为θ的光滑斜面上,存在着两个匀强磁场,ee′和ff′之间的区域的磁场方向垂直斜面向上,磁感应强度大小为B,ff′和gg′之间的区域的磁场方向垂直斜面向下,磁感应强度大小为2B,这两个磁场的宽度均为L,一个质量为m、电阻为R、边长也为L的正方形导线框,由静止开始沿斜面下滑,当ab边刚越过ee′进入磁场时,导线框恰好以速度v1做匀速直线运动;当ab边下滑到 ff′与gg′的中间位置时,线框又恰好以速度v2做匀速直线运动,从ab边进入ee′到ab边到达ff′和gg′的中间位置的过程中,线框的动能变化量为△Ek,重力对线框做功为W1,安培力对线框做功为W2,对该过程中的说法正确的有( )
在如图所示的倾角为θ的光滑斜面上,存在着两个匀强磁场,ee′和ff′之间的区域的磁场方向垂直斜面向上,磁感应强度大小为B,ff′和gg′之间的区域的磁场方向垂直斜面向下,磁感应强度大小为2B,这两个磁场的宽度均为L,一个质量为m、电阻为R、边长也为L的正方形导线框,由静止开始沿斜面下滑,当ab边刚越过ee′进入磁场时,导线框恰好以速度v1做匀速直线运动;当ab边下滑到 ff′与gg′的中间位置时,线框又恰好以速度v2做匀速直线运动,从ab边进入ee′到ab边到达ff′和gg′的中间位置的过程中,线框的动能变化量为△Ek,重力对线框做功为W1,安培力对线框做功为W2,对该过程中的说法正确的有( )| A. | v1:v2=6:1 | B. | v1:v2=9:1 | ||
| C. | 最大瞬时加速度为7gsinθ | D. | △Ek=W1-W2 |
分析 线框的ab边刚越过ee′进入磁场后做匀速直线运动,对线框受力分析,由共点力的平衡条件可得出线框的速度v1;
ab边到达ff′与gg′之间的中间位置时仍做匀速直线运动,同理由共点力的平衡条件可得出线框的速度v2;由动能定理求解动能的增加量.由牛顿第二定律和安培力与速度的关系式求解加速度.
解答 解:AB、线框的ab边刚越过ee′时,回路中的感应电动势为:E1=BLv1;
感应电流为:I1=$\frac{{E}_{1}}{R}$;
线框受到的安培力大小为:F1=BI1L=$\frac{{B}^{2}{L}^{2}{v}_{1}}{R}$
根据平衡条件有:mgsinθ-F1=0
解得:v1=$\frac{mgRsinθ}{{B}^{2}{L}^{2}}$;
当ab边到达gg′与ff′间的中间置时,回路中感应电动势为:E2=BLv2+2BLv2=3BLv2;
感应电流为:I2=$\frac{{E}_{2}}{R}$
线框受到的安培力大小为:F2=2BI2L+BI2L=3BI2L=$\frac{9{B}^{2}{L}^{2}{v}_{2}}{R}$
由平衡条件有:mgsinθ-$\frac{9{B}^{2}{L}^{2}{v}_{2}}{R}$=0
解得:v2=$\frac{mgRsinθ}{9{B}^{2}{L}^{2}}$;则v1:v2=9:1.故A错误,B正确.
C、线框的ab边刚进入ff′与gg′间磁场时加速度最大,结合上题的结果可知,此时线框所受的安培力:F′=$\frac{9{B}^{2}{L}^{2}{v}_{1}}{R}$
由上题:v1=$\frac{mgRsinθ}{{B}^{2}{L}^{2}}$,
则得:F′=9mgsinθ
根据牛顿第二定律得:F′-mgsinθ=ma,
得:a=8gsinθ,故C错误.
D、根据动能定理可知,△Ek=W1+W2,故D错误.
故选:B.
点评 导体切割磁感线运动时,要抓住受力平衡及能量的转化及守恒的关系进行分析判断,关键要准确求出安培力与速度的关系式,注意ab和cd两边都可能受安培力.

 把一个平行玻璃板压在另一个平行玻璃板上,一端用薄片垫起,构成空气劈尖,让单色光从上方射入(如图),这时可以看到亮暗相间的条纹,下面关于条纹的说法中正确的是( )
把一个平行玻璃板压在另一个平行玻璃板上,一端用薄片垫起,构成空气劈尖,让单色光从上方射入(如图),这时可以看到亮暗相间的条纹,下面关于条纹的说法中正确的是( )| A. | 将薄片向着劈尖移动使劈角变大时,条纹变疏 | |
| B. | 将上玻璃板平行上移,条纹远离劈尖移动 | |
| C. | 将上玻璃板平行上移,条纹不动 | |
| D. | 将薄片远离劈尖移动使劈角变小时,条纹变疏 |
| A. | 只有红色和绿色的干涉条纹,其它颜色的双缝干涉条纹消失 | |
| B. | 红色和绿色的干涉条纹消失,其它颜色的干涉条纹仍然存在 | |
| C. | 任何颜色的干涉条纹都不存在,但屏上仍有亮光 | |
| D. | 屏上无任何亮光 |
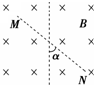 地面附近空间中存在着水平方向的匀强电场和匀强磁场,已知磁场方向垂直纸面向里,一个带电油滴沿着一条与竖直方向成α角的直线MN运动,如图所示,由此可以判断( )
地面附近空间中存在着水平方向的匀强电场和匀强磁场,已知磁场方向垂直纸面向里,一个带电油滴沿着一条与竖直方向成α角的直线MN运动,如图所示,由此可以判断( )| A. | 油滴一定做匀速运动 | |
| B. | 油滴可以做变速运动 | |
| C. | 如果油滴带正电,它是从N点运动到M点 | |
| D. | 如果油滴带正电,它是从M点运动到N点 |
 传感器是把非电学量(如速度、温度、压力等)的变化转化成电学量变化的一种元件,在自动控制中有着相当广泛的应用,如图所示,是一种测定液面高度的电容式传感器示意图,金属芯线与导电的液体形成一个电容器,从电容C的大小变化就能反映导电液面的升降情况,两者的关系是( )
传感器是把非电学量(如速度、温度、压力等)的变化转化成电学量变化的一种元件,在自动控制中有着相当广泛的应用,如图所示,是一种测定液面高度的电容式传感器示意图,金属芯线与导电的液体形成一个电容器,从电容C的大小变化就能反映导电液面的升降情况,两者的关系是( )| A. | C增大表示h增大 | B. | C增大表示h减小 | C. | C减小表示h增大 | D. | C减小表示h减小 |
 一同学用如图所示装置研究感应电流的方向与引起感应电流的磁场方向的关系,已知电流从a接线柱流入电流表时,电流表指针右偏,实验时,磁场方向、磁铁运动情况及电流表指针偏转情况记录在表中.
一同学用如图所示装置研究感应电流的方向与引起感应电流的磁场方向的关系,已知电流从a接线柱流入电流表时,电流表指针右偏,实验时,磁场方向、磁铁运动情况及电流表指针偏转情况记录在表中.| 实验序号 | 磁场方向 | 磁铁运动情况 | 指针偏转情况 |
| 1 | 向下 | 插入 | 右偏 |
| 2 | 向下 | 拔出 | 左偏 |
| 3 | 向上 | 插入 | 左偏 |
| 4 | 向上 | 拔出 | 右偏 |
②由实验2、4得出的结论是:穿过闭合回路的磁通量减小时,感应电流的磁场与原磁场方向相同.
③由实验1、2、3、4得出的结论是:感应电流的磁场总是阻碍引起感应电流的磁场的变化.

 某学生在做实验中,忘记记下小球做平抛运动的起点位置O,若A为小球运动一段时间后的位置,试根据图中的B点(20cm,15cm)、C点(40cm,40cm),求出小球做平抛运动的起点位置O的坐标(x=-20cmy=-5cm)(g=10m/s2)
某学生在做实验中,忘记记下小球做平抛运动的起点位置O,若A为小球运动一段时间后的位置,试根据图中的B点(20cm,15cm)、C点(40cm,40cm),求出小球做平抛运动的起点位置O的坐标(x=-20cmy=-5cm)(g=10m/s2) 如图所示,质量M=0.2kg的长板静止在水平地面上,与地面间动摩擦因数μ1=0.1,另一质量m=0.1kg的小滑块以v0=0.9m/s初速滑上长木板,滑块与长木板间动摩擦因数μ2=0.4,求小滑块自滑上长板到最后静止(仍在木板上)的过程中,它相对于地运动的路程.
如图所示,质量M=0.2kg的长板静止在水平地面上,与地面间动摩擦因数μ1=0.1,另一质量m=0.1kg的小滑块以v0=0.9m/s初速滑上长木板,滑块与长木板间动摩擦因数μ2=0.4,求小滑块自滑上长板到最后静止(仍在木板上)的过程中,它相对于地运动的路程.