题目内容
3. 如图甲所示,一质量为M的长木板静置于光滑水平面上,其上放置一质量为m的小滑块.木板受到随时间t变化的水平拉力F作用时,用传感器测出其加速度a,得到如图乙所示的a-F图.取g=10m/s2,则( )
如图甲所示,一质量为M的长木板静置于光滑水平面上,其上放置一质量为m的小滑块.木板受到随时间t变化的水平拉力F作用时,用传感器测出其加速度a,得到如图乙所示的a-F图.取g=10m/s2,则( )| A. | 滑块的质量m=2 kg | B. | 木板的质量M=6 kg | ||
| C. | 当F=8 N时滑块加速度为2 m/s2 | D. | 滑块与木板间动摩擦因数为0.1 |
分析 当拉力较小时,m和M保持相对静止一起做匀加速直线运动,当拉力达到一定值时,m和M发生相对滑动,结合牛顿第二定律,运用整体和隔离法分析.
解答 解:A、当F等于6N时,加速度为:a=1m/s2,对整体分析,由牛顿第二定律有:F=(M+m)a,代入数据解得:M+m=6kg,当F大于6N时,根据牛顿第二定律得:a=$\frac{F-μmg}{M}$=$\frac{1}{M}$F-$\frac{μmg}{M}$,由图示图象可知,图线的斜率:k=$\frac{1}{M}$=$\frac{△a}{△F}$=$\frac{1}{6-4}$=$\frac{1}{2}$,解得:M=2kg,滑块的质量为:m=4kg.故AB错误.
C、根据F大于6N的图线知,F=4时,a=0,即:0=$\frac{1}{2}$×F-$\frac{μ×40}{2}$,代入数据解得:μ=0.1,由图示图象可知,当F=8N时,滑块与木板相对滑动,滑块的加速度为:a=μg=1m/s2.故C错误,D正确.
故选:D.
点评 本题考查牛顿第二定律与图象的综合,知道滑块和木板在不同拉力作用下的运动规律是解决本题的关键,掌握处理图象问题的一般方法,通常通过图线的斜率和截距入手分析.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
13.质量为2m的物体A,以一定的速度沿光滑水平面运动,与一静止的物体B碰撞后粘为一体继续运动,它们共同的速度为碰撞前A的速度的$\frac{2}{3}$,则物体B的质量为( )
| A. | m | B. | 2m | C. | 3m | D. | $\frac{2}{3}$m |
11.物体在自由下落过程中,重力做了40J的功,则有( )
| A. | 动能减少了40J | B. | 重力势能增加了40J | ||
| C. | 机械能增加了40J | D. | 机械能保持不变 |
18.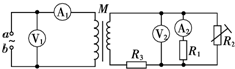 如图所示,M是一小型理想变压器,接线柱a、b接在电压u=311sin 314t(V)的正弦交变电源上.变压器右侧部分为一火警报警系统原理图,其中R2为用半导体热敏材料制成的传感器,电流表A2为值班室的显示器,显示通过R1的电流,电压表V2显示加在报警器上的电压(报警器未画出),R3为一定值电阻.当传感器R2所在处出现火警时(R2阻值变小),以下说法中正确的是( )
如图所示,M是一小型理想变压器,接线柱a、b接在电压u=311sin 314t(V)的正弦交变电源上.变压器右侧部分为一火警报警系统原理图,其中R2为用半导体热敏材料制成的传感器,电流表A2为值班室的显示器,显示通过R1的电流,电压表V2显示加在报警器上的电压(报警器未画出),R3为一定值电阻.当传感器R2所在处出现火警时(R2阻值变小),以下说法中正确的是( )
 如图所示,M是一小型理想变压器,接线柱a、b接在电压u=311sin 314t(V)的正弦交变电源上.变压器右侧部分为一火警报警系统原理图,其中R2为用半导体热敏材料制成的传感器,电流表A2为值班室的显示器,显示通过R1的电流,电压表V2显示加在报警器上的电压(报警器未画出),R3为一定值电阻.当传感器R2所在处出现火警时(R2阻值变小),以下说法中正确的是( )
如图所示,M是一小型理想变压器,接线柱a、b接在电压u=311sin 314t(V)的正弦交变电源上.变压器右侧部分为一火警报警系统原理图,其中R2为用半导体热敏材料制成的传感器,电流表A2为值班室的显示器,显示通过R1的电流,电压表V2显示加在报警器上的电压(报警器未画出),R3为一定值电阻.当传感器R2所在处出现火警时(R2阻值变小),以下说法中正确的是( )| A. | A1的示数增大,A2的示数增大 | B. | A1的示数增大,A2的示数减小 | ||
| C. | V1的示数不变,V2的示数减少 | D. | V1的示数不变,V2的示数不变 |
8. 如图所示,有一光滑轨道ABC,AB部分为半径为R的$\frac{1}{4}$圆弧,BC部分水平,质量均为m的小球a、b固定在竖直轻杆的两端,轻杆长为R,不计小球大小.开始时a球处在圆弧上端A点,由静止释放小球和轻杆,使其沿光滑轨道下滑,下列说法正确的是( )
如图所示,有一光滑轨道ABC,AB部分为半径为R的$\frac{1}{4}$圆弧,BC部分水平,质量均为m的小球a、b固定在竖直轻杆的两端,轻杆长为R,不计小球大小.开始时a球处在圆弧上端A点,由静止释放小球和轻杆,使其沿光滑轨道下滑,下列说法正确的是( )
 如图所示,有一光滑轨道ABC,AB部分为半径为R的$\frac{1}{4}$圆弧,BC部分水平,质量均为m的小球a、b固定在竖直轻杆的两端,轻杆长为R,不计小球大小.开始时a球处在圆弧上端A点,由静止释放小球和轻杆,使其沿光滑轨道下滑,下列说法正确的是( )
如图所示,有一光滑轨道ABC,AB部分为半径为R的$\frac{1}{4}$圆弧,BC部分水平,质量均为m的小球a、b固定在竖直轻杆的两端,轻杆长为R,不计小球大小.开始时a球处在圆弧上端A点,由静止释放小球和轻杆,使其沿光滑轨道下滑,下列说法正确的是( )| A. | a、b两球下滑过程速度始终大小相等 | |
| B. | a、b两球和轻杆组成的系统在下滑过程中机械能保持不变 | |
| C. | a、b滑到水平轨道上时速度为$\sqrt{2gR}$ | |
| D. | 从释放到a、b滑到水平轨道上,整个过程中轻杆对a球做的功为$\frac{mgR}{2}$ |
15. 如图所示,三颗质量均为m的地球同步卫星等间隔分布在半径为r的圆轨道上,设地球质量为M,半径为R.下列说法正确的是( )
如图所示,三颗质量均为m的地球同步卫星等间隔分布在半径为r的圆轨道上,设地球质量为M,半径为R.下列说法正确的是( )
 如图所示,三颗质量均为m的地球同步卫星等间隔分布在半径为r的圆轨道上,设地球质量为M,半径为R.下列说法正确的是( )
如图所示,三颗质量均为m的地球同步卫星等间隔分布在半径为r的圆轨道上,设地球质量为M,半径为R.下列说法正确的是( )| A. | 地球对一颗卫星的引力大小为$\frac{GMm}{(r-R)^{2}}$ | |
| B. | 两颗卫星之间的引力大小为$\frac{\sqrt{3}G{m}^{2}}{3{r}^{2}}$ | |
| C. | 一颗卫星对地球的引力大小为$\frac{GMm}{{r}^{2}}$ | |
| D. | 三颗卫星对地球引力的合力大小为$\frac{3GMm}{{r}^{2}}$ |
13. 如图所示,吊篮A,物体B、物体C的质量分别为m、3m、2m.B和C分别固定在弹簧两端,弹簧的质量不计.B和C在吊篮的水平底板上处于静止状态.将悬挂吊篮的轻绳剪断的瞬间( )
如图所示,吊篮A,物体B、物体C的质量分别为m、3m、2m.B和C分别固定在弹簧两端,弹簧的质量不计.B和C在吊篮的水平底板上处于静止状态.将悬挂吊篮的轻绳剪断的瞬间( )
 如图所示,吊篮A,物体B、物体C的质量分别为m、3m、2m.B和C分别固定在弹簧两端,弹簧的质量不计.B和C在吊篮的水平底板上处于静止状态.将悬挂吊篮的轻绳剪断的瞬间( )
如图所示,吊篮A,物体B、物体C的质量分别为m、3m、2m.B和C分别固定在弹簧两端,弹簧的质量不计.B和C在吊篮的水平底板上处于静止状态.将悬挂吊篮的轻绳剪断的瞬间( )| A. | 吊篮A的加速度大小为2g | B. | 物体B的加速度大小为g | ||
| C. | 物体C的加速度大小为2g | D. | A、B、C的加速度大小都等于g |


 某波源S发出一列简谐横波,波源S的振动图象如图所示.在波的传播方向上有A、B两点,他们到S的距离分别为45m和55m.测得A、B两点开始振动的时间间隔为1.0s.由此可知
某波源S发出一列简谐横波,波源S的振动图象如图所示.在波的传播方向上有A、B两点,他们到S的距离分别为45m和55m.测得A、B两点开始振动的时间间隔为1.0s.由此可知