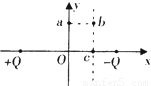题目内容
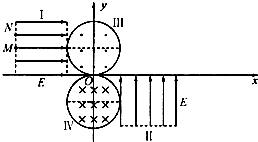 如图所示,真空中一平面直角坐标系xOy内,存在着两个边长为L的正方形匀强电场区域I、II和两个直径为L的圆形匀强磁场区域III,IV.电场的场强大小均为E,区域I的 场强方向沿x轴正方向,其下边界在x轴上,右边界刚好与区域III的边界相切;区域II的场 强方向沿y轴正方向,其上边界在x轴上,左边界刚好与区域仅的边界相切.磁场的磁感应强度大小均为2
如图所示,真空中一平面直角坐标系xOy内,存在着两个边长为L的正方形匀强电场区域I、II和两个直径为L的圆形匀强磁场区域III,IV.电场的场强大小均为E,区域I的 场强方向沿x轴正方向,其下边界在x轴上,右边界刚好与区域III的边界相切;区域II的场 强方向沿y轴正方向,其上边界在x轴上,左边界刚好与区域仅的边界相切.磁场的磁感应强度大小均为2
|
| L |
| 2 |
| L |
| 2 |
| 3L |
| 2 |
| 1 |
| 2 |
| 3L |
| 2 |
2+
| ||
| 4 |
(1)粒子离开电场I时的速度大小.
(2)粒子M击中感光板的位置坐标.
(3)粒子N在磁场中运动的时间.
分析:(1)粒子在区域Ⅰ中运动时,由动能定理求解粒子离开电场I时的速度大小.
(2)粒子在磁场中做匀速圆周运动,由牛顿第二定律求出轨迹半径.因M运动的轨道半径与磁场区域的半径相同,故M在磁场Ⅲ中运动四分之一周期后经过原点进入磁场Ⅳ,再运动四分之一周期后平行于x轴正方向离开磁场,然后进入电场Ⅱ做类平抛运动.假设M射出电场后再打在x轴的感光板上,运用类平抛运动的规律求解粒子M击中感光板的位置坐标.
(3)N做圆周运动的轨道半径与磁场区域的半径相同,分析可得N将从b点进入磁场,由坐标原点O离开磁场Ⅲ进入磁场Ⅳ,然后从d点离开磁场Ⅳ,画出其运动轨迹,运用几何知识求出轨迹对应的圆心角,结合对称性即可求得粒子N在磁场中运动的时间.
(2)粒子在磁场中做匀速圆周运动,由牛顿第二定律求出轨迹半径.因M运动的轨道半径与磁场区域的半径相同,故M在磁场Ⅲ中运动四分之一周期后经过原点进入磁场Ⅳ,再运动四分之一周期后平行于x轴正方向离开磁场,然后进入电场Ⅱ做类平抛运动.假设M射出电场后再打在x轴的感光板上,运用类平抛运动的规律求解粒子M击中感光板的位置坐标.
(3)N做圆周运动的轨道半径与磁场区域的半径相同,分析可得N将从b点进入磁场,由坐标原点O离开磁场Ⅲ进入磁场Ⅳ,然后从d点离开磁场Ⅳ,画出其运动轨迹,运用几何知识求出轨迹对应的圆心角,结合对称性即可求得粒子N在磁场中运动的时间.
解答: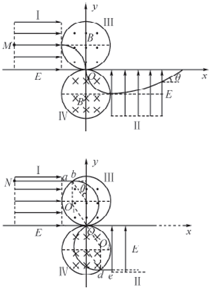 解:(1)粒子在区域Ⅰ中运动,由动能定理得:
解:(1)粒子在区域Ⅰ中运动,由动能定理得:
qEL=
m
解得 v0=
.
(2)粒子在磁场中做匀速圆周运动,由牛顿第二定律得:
qv0B=m
因B=2
,
故得 r=
=
因M运动的轨道半径与磁场区域的半径相同,故M在磁场Ⅲ中运动四分之一周期后经过原点进入磁场Ⅳ,再运动四分之一周期后平行于x轴正方向离开磁场,然后进入电场Ⅱ做类平抛运动.
假设M射出电场后再打在x轴的感光板上,则:
M在电场中运动时间 t=
沿电场力位移 y=
at2=
×
×(
)2=
L<
L;
所以假设成立,运动轨迹如右图所示.
沿电场方向的速度 vy=at=
速度偏向角的正切 tanθ=
=
设出电场后沿x轴方向的位移为x1,则
tanθ=
,
所以 x1=
M击中感光板的横坐标为 x=
+L+x1=2L,位置坐标为(2L,0);
(3)N做圆周运动的轨道半径与磁场区域的半径相同,分析可得N将从b点进入磁场,由坐标原点O离开磁场Ⅲ进入磁场Ⅳ,然后从d点离开磁场Ⅳ,其部分轨迹如右图所示.
在磁场Ⅲ中,由几何关系得:cosθ=
=
所以 θ=30°,圆弧对应的圆心角 φ=180°-30°=150°
粒子在运动的周期 T=
=π
所以粒子在磁场Ⅲ中运动的时间 t′=
T=
由对称关系得粒子在磁场Ⅲ、Ⅳ中运动时间相同
故粒子在磁场中运动的时间为 t″=2t′=
;
答:
(1)粒子离开电场I时的速度大小是
.
(2)粒子M击中感光板的位置坐标是(2L,0).
(3)粒子N在磁场中运动的时间为
.
 解:(1)粒子在区域Ⅰ中运动,由动能定理得:
解:(1)粒子在区域Ⅰ中运动,由动能定理得:qEL=
| 1 |
| 2 |
| v | 2 0 |
解得 v0=
|
(2)粒子在磁场中做匀速圆周运动,由牛顿第二定律得:
qv0B=m
| ||
| r |
因B=2
|
故得 r=
| mv0 |
| qB |
| L |
| 2 |
因M运动的轨道半径与磁场区域的半径相同,故M在磁场Ⅲ中运动四分之一周期后经过原点进入磁场Ⅳ,再运动四分之一周期后平行于x轴正方向离开磁场,然后进入电场Ⅱ做类平抛运动.
假设M射出电场后再打在x轴的感光板上,则:
M在电场中运动时间 t=
| L |
| v0 |
沿电场力位移 y=
| 1 |
| 2 |
| 1 |
| 2 |
| qE |
| m |
| L |
| v0 |
| 1 |
| 4 |
| 1 |
| 2 |
所以假设成立,运动轨迹如右图所示.
沿电场方向的速度 vy=at=
|
速度偏向角的正切 tanθ=
| vy |
| v0 |
| 1 |
| 2 |
设出电场后沿x轴方向的位移为x1,则
tanθ=
| ||||
| x1 |
所以 x1=
| L |
| 2 |
M击中感光板的横坐标为 x=
| L |
| 2 |
(3)N做圆周运动的轨道半径与磁场区域的半径相同,分析可得N将从b点进入磁场,由坐标原点O离开磁场Ⅲ进入磁场Ⅳ,然后从d点离开磁场Ⅳ,其部分轨迹如右图所示.
在磁场Ⅲ中,由几何关系得:cosθ=
| ||||
|
| ||
| 2 |
所以 θ=30°,圆弧对应的圆心角 φ=180°-30°=150°
粒子在运动的周期 T=
2π×
| ||
| v0 |
|
所以粒子在磁场Ⅲ中运动的时间 t′=
| φ |
| 360° |
| 5π |
| 12 |
|
由对称关系得粒子在磁场Ⅲ、Ⅳ中运动时间相同
故粒子在磁场中运动的时间为 t″=2t′=
| 5π |
| 6 |
|
答:
(1)粒子离开电场I时的速度大小是
|
(2)粒子M击中感光板的位置坐标是(2L,0).
(3)粒子N在磁场中运动的时间为
| 5π |
| 6 |
|
点评:解决本题的关键是画出粒子的运动轨迹,灵活运用几何知识轨迹半径,确定轨迹对应的圆心角,即可求得粒子在磁场中运动的时间.

练习册系列答案
相关题目
 如图所示,真空中有一匀强电场和水平面成一定角度斜向上,一个电荷量为Q=-5×10-6 C的点电荷固定于电场中的O处,在a处有一个质量为m=9×10-3 kg、电荷量为q=2×10-8C的点电荷恰能处于静止,a与O在同一水平面上,且相距为r=0.1m.现用绝缘工具将q搬到与a在同一竖直平面上的b点,Oa=Ob且相互垂直,在此过程中外力至少做功为( )
如图所示,真空中有一匀强电场和水平面成一定角度斜向上,一个电荷量为Q=-5×10-6 C的点电荷固定于电场中的O处,在a处有一个质量为m=9×10-3 kg、电荷量为q=2×10-8C的点电荷恰能处于静止,a与O在同一水平面上,且相距为r=0.1m.现用绝缘工具将q搬到与a在同一竖直平面上的b点,Oa=Ob且相互垂直,在此过程中外力至少做功为( ) (2011?合肥模拟)如图所示,真空中苻平而盘角坐标系.xOy,在x轴上固定着关于O点对称的等量异种点电荷和+Q和-Q,a是y轴上的一点,c是.x轴上的一点,ab,bc分别与X轴和y轴平行.将一个正的试探电荷+q沿aOcba移动一周,则( )
(2011?合肥模拟)如图所示,真空中苻平而盘角坐标系.xOy,在x轴上固定着关于O点对称的等量异种点电荷和+Q和-Q,a是y轴上的一点,c是.x轴上的一点,ab,bc分别与X轴和y轴平行.将一个正的试探电荷+q沿aOcba移动一周,则( ) 如图所示,真空中有一平行板电容器,两极板分别用锌板和铜板制成(锌板和铜板的极限频率分别为υ1和υ2,且υ1<υ2),板面积为S,间距为d.锌板与灵敏静电计相连,锌板和铜板原来都不带电.现用频率为υ(υ1<υ<υ2)的单色光持续照射两板内表面,假设光电子全部到达另一极板,则电容器的最终带电荷量Q正比于( )
如图所示,真空中有一平行板电容器,两极板分别用锌板和铜板制成(锌板和铜板的极限频率分别为υ1和υ2,且υ1<υ2),板面积为S,间距为d.锌板与灵敏静电计相连,锌板和铜板原来都不带电.现用频率为υ(υ1<υ<υ2)的单色光持续照射两板内表面,假设光电子全部到达另一极板,则电容器的最终带电荷量Q正比于( )