题目内容
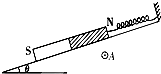
【题目】如图所示,固定且足够长的平行光滑金属导轨EF、PQ所在平面的倾角θ=53°,导轨的下端E、P之间接有R=1Ω的定值电阻,导轨间距L=1m,导轨的电阻不计,导轨上垂直于导轨的虚线上方有垂直于导轨平面向上的匀强磁场,磁场的磁感应强度大小B=1T,在虚线下方的导轨上放一垂直于导轨的金属棒ab,金属棒ab的质量m=1kg,有效电阻r=0.5Ω,长度也为L=1m,将金属棒ab与绕过导轨上端的定滑轮的细线连接,定滑轮与金属棒ab间的细线与导轨平行,细线的另一端吊着一个重物,重物的质量也为m=1kg,释放重物,细线带着金属棒ab向上运动,金属棒ab运动过程中,始终与导轨垂直,且与导轨接触良好,开始时金属棒ab到虚线的距离s=0.5m,重力加速度g=10/s2 , sin53°=0.8,cos53°=0.6,求: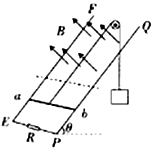
(1)金属棒ab刚进入磁场时的速度;
(2)金属棒ab刚进入磁场时的加速度;
(3)金属棒ab在磁场中做匀速运动时的速度.
【答案】
(1)解:根据机械能守恒,有:mgs﹣mgssinθ= ![]() ,
,
解得v1=1m/s;
答:金属棒ab刚进入磁场时的速度为1m/s;
(2)解:刚进入磁场时,对于重物根据牛顿第二定律有:mg﹣T=ma,
对于金属棒根据牛顿第二定律可得:T﹣mgsinθ﹣F安=ma,
根据安培力的计算公式可得:F安=BIL= ![]() ,
,
联立解得加速度:a= ![]() ;
;
答:金属棒ab刚进入磁场时的加速度为 ![]() ;
;
(3)解:设金属棒ab在磁场中匀速运动的速度为v2,则有:mg﹣mgsinθ﹣ ![]() =0,
=0,
解得v2=3m/s.
答:金属棒ab在磁场中做匀速运动时的速度为3m/s.
【解析】(1)导体棒进入磁场之前只有重力做功,机械能守恒,根据机械能守恒定律列方程求解;
(2)对重物和金属棒分别根据牛顿第二定律列方程求解加速度;
(3)金属棒匀速运动受力平衡,根据共点力的平衡条件列方程求解匀速运动的速度大小.
【考点精析】根据题目的已知条件,利用机械能守恒及其条件和电磁感应与电路的相关知识可以得到问题的答案,需要掌握在只有重力(和弹簧弹力)做功的情形下,物体动能和重力势能(及弹性势能)发生相互转化,但机械能的总量保持不变;用法拉第电磁感应定律和楞次定律确定感应电动势的大小和方向;画等效电路;运用全电路欧姆定律,串并联电路性质,电功率等公式联立求解.