题目内容
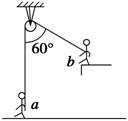
如图4－3－12所示，一根跨过光滑定滑轮的轻绳，两端各有一杂技演员(可视为质点)．a站在地面上，b从图示的位置由静止开始向下摆动，运动过程中绳始终处于伸直状态．当演员b摆至最低点时，a刚好对地面无压力，则演员a的质量与演员b的质量之比为( )．
A．1∶1 B．2∶1 C．3∶1 D．4∶1
解析 设b摆至最低点时的速度为v，b侧所拉绳子长度为l，由机械能守恒定律可得：mgl(1－cos 60°)＝
mv2，解得v＝
.设b摆至最低点时绳子的拉力为FT，由牛顿第二定律得：FT－mbg＝mb
，解得FT＝2mbg，对演员a有FT＝mag，所以，演员a的质量与演员b的质量之比为2∶1.
答案 B
某同学利用如图4－5－12所示的实验装置验证机械能守恒定律．该同学经正确操作得到打点纸带，在纸带后段每两个计时间隔取一个计数点，依次为1、2、3、4、5、6、7，测量各计数点到第一个点的距离h，并正确求出打相应点时的速度v.各计数点对应的数据见下表：
| 计数点 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| h/m | 0.124 | 0.194 | 0.279 | 0.380 | 0.497 | 0.630 | 0.777 |
| v/(m·s－1) |
| 1.94 | 2.33 | 2.73 | 3.13 | 3.50 | |
| v2/(m2·s－2) |
| 3.76 | 5.43 | 7.45 | 9.80 | 12.3 |
请在图4－5－13坐标中，描点作出v2－h图线；由图线可知，重锤下落的加速度g′＝________ m/s2(保留三位有效数字)；若当地的重力加速度g＝9.80 m/s2，根据作出的图线，能粗略验证自由下落的重锤机械能守恒的依据是____________________________________________．
图4－5－12
图4－5－13