题目内容
 如图所示,AC、BC为位于竖直平面内的两根光滑细杆,A、B、C三点恰位于同一圆周上,C为该圆周的最低点,O为圆心.a、b为套在细杆上的两个小环,现让两环同时由A、B两点从静止开始下滑,则( )
如图所示,AC、BC为位于竖直平面内的两根光滑细杆,A、B、C三点恰位于同一圆周上,C为该圆周的最低点,O为圆心.a、b为套在细杆上的两个小环,现让两环同时由A、B两点从静止开始下滑,则( )分析:小环沿杆下滑做匀加速直线运动,找出最高点D,设∠ACD为θ,求出小球运动的加速度和位移,根据匀加速直线运动位移时间公式表示出时间即可求解.
解答:解:
 小环在杆上做初速度为0的匀加速直线运动,如图,∠ACD=θ,小环在杆上下滑时的加速度a=gcosθ,令圆的半径为R,则根据几何关系有:
小环在杆上做初速度为0的匀加速直线运动,如图,∠ACD=θ,小环在杆上下滑时的加速度a=gcosθ,令圆的半径为R,则根据几何关系有:
AC=2Rcosθ
小环在AC上下滑的加速度a=gcosθ,因为小环做初速度为0的匀加速直线运动,根据位移时间关系有:
AC=
at2
即:2Rcosθ=
gcosθ?t2得:沿杆滑的时间t=
与杆的倾角θ无关,故C正确,ABD错误.
故选C.
 小环在杆上做初速度为0的匀加速直线运动,如图,∠ACD=θ,小环在杆上下滑时的加速度a=gcosθ,令圆的半径为R,则根据几何关系有:
小环在杆上做初速度为0的匀加速直线运动,如图,∠ACD=θ,小环在杆上下滑时的加速度a=gcosθ,令圆的半径为R,则根据几何关系有:AC=2Rcosθ
小环在AC上下滑的加速度a=gcosθ,因为小环做初速度为0的匀加速直线运动,根据位移时间关系有:
AC=
| 1 |
| 2 |
即:2Rcosθ=
| 1 |
| 2 |
|
故选C.
点评:本题主要考查了匀加速直线运动位移时间公式的直接应用,要求同学们能正确对小球进行受力分析,求出加速度,难度适中.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,AC和BC是两个固定的斜面,斜面的顶端在同一竖直线上.质量相同的两个小滑块分别自斜面AC和BC的顶端由静止开始下滑,小滑块与斜面间的动摩擦因数相同.从斜面AC上滑下的滑块滑至底部C点时的动能为Ek1,下滑过程中克服摩擦力所做的功为W1;从斜面BC上滑下的滑块滑至底部C点时的动能为Ek2,下滑过程中克服摩擦力所做的功为W2,则( )
如图所示,AC和BC是两个固定的斜面,斜面的顶端在同一竖直线上.质量相同的两个小滑块分别自斜面AC和BC的顶端由静止开始下滑,小滑块与斜面间的动摩擦因数相同.从斜面AC上滑下的滑块滑至底部C点时的动能为Ek1,下滑过程中克服摩擦力所做的功为W1;从斜面BC上滑下的滑块滑至底部C点时的动能为Ek2,下滑过程中克服摩擦力所做的功为W2,则( ) 如图所示,AC和BC两轻绳共同悬挂一质量为m的物体,若保持AC绳的方向不变,AC与竖直向上方向的夹角为60°,改变BC绳的方向,试求:
如图所示,AC和BC两轻绳共同悬挂一质量为m的物体,若保持AC绳的方向不变,AC与竖直向上方向的夹角为60°,改变BC绳的方向,试求: 如图所示,固定在水平面上的光滑半球,球心O的正上方固定一个小定滑轮C,细绳一端拴一小球,小球置于半球面上的A点,另一端绕过定滑轮拴另一个半径相同的小球,小球置于半球面上的B点,如图所示,AC与BC的长度比为6:5.则AB两个小球的质量比为( )
如图所示,固定在水平面上的光滑半球,球心O的正上方固定一个小定滑轮C,细绳一端拴一小球,小球置于半球面上的A点,另一端绕过定滑轮拴另一个半径相同的小球,小球置于半球面上的B点,如图所示,AC与BC的长度比为6:5.则AB两个小球的质量比为( )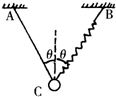 一根细绳与一个轻弹簧,上端分别固定在A、B两点,下端C点共同拉住一个小钢球,如图所示,AC、BC与竖直方向的夹角均为θ,则( )
一根细绳与一个轻弹簧,上端分别固定在A、B两点,下端C点共同拉住一个小钢球,如图所示,AC、BC与竖直方向的夹角均为θ,则( )