题目内容
如图所示，AC和BC是两个固定的斜面，斜面的顶端在同一竖直线上．质量相同的两个小滑块分别自斜面AC和BC的顶端由静止开始下滑，小滑块与斜面间的动摩擦因数相同．从斜面AC上滑下的滑块滑至底部C点时的动能为Ek1，下滑过程中克服摩擦力所做的功为W1；从斜面BC上滑下的滑块滑至底部C点时的动能为Ek2，下滑过程中克服摩擦力所做的功为W2，则（ ）分析：根据摩擦力做功的公式比较在两个斜面上物体克服摩擦力所做的功，再通过动能定理比较到达底部的动能
解答：解：设斜面的倾角为θ，滑动摩擦力大小为f=μmgcosθ，
则物体克服摩擦力所做的功为w=μmgscosθ．而scosθ相同，所以克服摩擦力做功相等．
根据动能定理得：mgh-μmgscosθ=EK-0，
在AC斜面上滑动时重力做功多，克服摩擦力做功相等，
则在AC面上滑到底端的动能大于在BC面上滑到底端的动能，即Ek1＞Ek2．
故B正确，A、C、D错误．
故选：B
则物体克服摩擦力所做的功为w=μmgscosθ．而scosθ相同，所以克服摩擦力做功相等．
根据动能定理得：mgh-μmgscosθ=EK-0，
在AC斜面上滑动时重力做功多，克服摩擦力做功相等，
则在AC面上滑到底端的动能大于在BC面上滑到底端的动能，即Ek1＞Ek2．
故B正确，A、C、D错误．
故选：B
点评：解决本题的关键要掌握功的公式W=Fscosθ，以及灵活运用动能定理．
练习册系列答案
相关题目
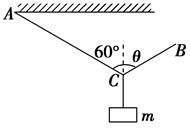
如图所示，AC和BC两轻绳共同悬挂一质量为m的物体，若保持AC绳的方向不变，AC与竖直向上方向的夹角为60°，改变BC绳的方向，试求：
如图所示，AC和BC是两个固定的斜面，斜面的顶端在同一竖直线上。质量相同的两个物体分别自斜面AC和BC的顶端由静止开始下滑，物体与斜面间的动摩擦因数相同。从斜面AC上滑下的物体滑至底部C点时的动能为Ek1，下滑过程中克服摩擦力所做的功为W1；从斜面BC上滑下的物体滑至底部C点时的动能为Ek2，下滑过程中克服摩擦力所做的功为W2，则（ ）
| A．Ek1< Ek2， W1 > W2 |
| B．Ek1> Ek2， W1 > W2 |
| C．Ek1> Ek2， W1 = W2 |
| D．Ek1< Ek2， W1< W2 |
如图所示，AC和BC是两个固定的斜面，斜面的顶端在同一竖直线上。质量相同的两个物体分别自斜面AC和BC的顶端由静止开始下滑，物体与斜面间的动摩擦因数相同。从斜面AC上滑下的物体滑至底部C点时的动能为Ek1，下滑过程中克服摩擦力所做的功为W1；从斜面BC上滑下的物体滑至底部C点时的动能为Ek2，下滑过程中克服摩擦力所做的功为W2，则（ ）
| A．Ek1< Ek2， W1 > W2 |
| B．Ek1> Ek2， W1 > W2 |
| C．Ek1> Ek2， W1 = W2 |
| D．Ek1< Ek2， W1< W2 |