题目内容
8.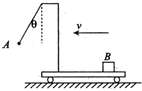 如图所示,带支架的平板小车沿水平面向左做直线运动,小球A用细线悬挂于支架前端,质量为m的物块B始终相对于小车静止地摆放在右端.B与小车平板间的动摩擦因数为μ.若某时刻观察到细线偏离竖直方向θ角,则此刻小车对物块B产生的作用力的大小和方向为( )
如图所示,带支架的平板小车沿水平面向左做直线运动,小球A用细线悬挂于支架前端,质量为m的物块B始终相对于小车静止地摆放在右端.B与小车平板间的动摩擦因数为μ.若某时刻观察到细线偏离竖直方向θ角,则此刻小车对物块B产生的作用力的大小和方向为( )| A. | mg,竖直向上 | B. | mg$\sqrt{1+{μ}^{2}}$,斜向左上方 | ||
| C. | mgtanθ,水平向右 | D. | mg$\sqrt{1+ta{n}^{2}θ}$,斜向右上方 |
分析 先以A为研究对象,根据牛顿第二定律求出加速度.再对B研究,由牛顿第二定律求解小车对物块B产生的摩擦力大小和方向,再对支持力进行合成,得到小车对B的作用力的大小和方向.
解答  解:以A为研究对象,分析受力如图,根据牛顿第二定律得:
解:以A为研究对象,分析受力如图,根据牛顿第二定律得:
mAgtanθ=mAa,
得:a=gtanθ,方向水平向右.
再对B研究得:小车对B的摩擦力为:f=ma=mgtanθ,方向水平向右,
小车对B的支持力大小为N=mg,方向竖直向上,
则小车对物块B产生的作用力的大小为:F=$\sqrt{{N}^{2}+{f}^{2}}$=mg$\sqrt{1+ta{n}^{2}θ}$,方向斜向右上方
故选:D
点评 本题要抓住小球、物块B和小车的加速度相同的特点,根据牛顿第二定律采用隔离法研究

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
18. 小型交流发电机中,矩形金属线圈在匀强磁场中匀速转动.产生的感应电动势与时间呈正弦函数关系,如图所示,此线圈与一个R=110Ω的电阻构成闭合电路,不计电路的其他电阻,下列说法中正确的是( )
小型交流发电机中,矩形金属线圈在匀强磁场中匀速转动.产生的感应电动势与时间呈正弦函数关系,如图所示,此线圈与一个R=110Ω的电阻构成闭合电路,不计电路的其他电阻,下列说法中正确的是( )
 小型交流发电机中,矩形金属线圈在匀强磁场中匀速转动.产生的感应电动势与时间呈正弦函数关系,如图所示,此线圈与一个R=110Ω的电阻构成闭合电路,不计电路的其他电阻,下列说法中正确的是( )
小型交流发电机中,矩形金属线圈在匀强磁场中匀速转动.产生的感应电动势与时间呈正弦函数关系,如图所示,此线圈与一个R=110Ω的电阻构成闭合电路,不计电路的其他电阻,下列说法中正确的是( )| A. | 电压有效值为220$\sqrt{2}$V | |
| B. | 电流的周期为0.01s | |
| C. | 如果在该电阻器两端并联一个交流电压表,该电压表的示数为220 V | |
| D. | 如果在该电路中串联一个交流电流表,该电流表的示数为2$\sqrt{2}$V |
19.关于重力势能与重力做功的下列说法中正确的是( )
| A. | 物体克服重力做的功等于重力势能的减少 | |
| B. | 在同一高度,将物体以相同的初速度沿不同方向从抛出到落地过程中,重力做的功相等,物体所减少的重力势能一定相等 | |
| C. | 重力势能等于零的物体,不可能对别的物体做功 | |
| D. | 用手托住一个物体匀速上举时,手的支持力做的功等于克服重力做的功与物体所增加的重力势能之和 |
16. 在做“探究功与物体速度变化的关系”的实验时,小车的质量为m,使用橡皮筋6根,每次增加一根,实验中W、v、v2的数据已填在下面表格中.
在做“探究功与物体速度变化的关系”的实验时,小车的质量为m,使用橡皮筋6根,每次增加一根,实验中W、v、v2的数据已填在下面表格中.
(1)在图甲乙两坐标系中选择合适的坐标系作出图象.
(2)从图象可以得出的实验结论是从乙图看出W∝v2.
 在做“探究功与物体速度变化的关系”的实验时,小车的质量为m,使用橡皮筋6根,每次增加一根,实验中W、v、v2的数据已填在下面表格中.
在做“探究功与物体速度变化的关系”的实验时,小车的质量为m,使用橡皮筋6根,每次增加一根,实验中W、v、v2的数据已填在下面表格中.| W | v/m•s-1 | v2/m2•s-2 |
| 0 | 0 | 0 |
| 1.00 | 0.80 | 0.64 |
| 2.00 | 1.10 | 1.21 |
| 3.00 | 1.28 | 1.64 |
| 4.00 | 1.53 | 2.34 |
| 5.00 | 1.76 | 3.10 |
| 6.00 | 1.89 | 3.57 |
(2)从图象可以得出的实验结论是从乙图看出W∝v2.
13.一列简谐横波,在t=0.6s时刻的图象如图甲所示,波上A质点的振动图象如图乙所示,则以下说法正确的是( )


| A. | 这列波沿x轴正方向传播,波速是$\frac{50}{3}$m/s | |
| B. | 从t=0.6s开始,紧接着的△t=0.6s时间内,A质点通过的路程是4m | |
| C. | 从t=0.6s开始,质点P比质点Q早0.4s到达波峰位置 | |
| D. | 从t=0.6s开始,再经0.15s质点Q第一次到达波谷位置 |
17. 如图所示,一物体从A点先后沿光滑路径Ⅰ、Ⅱ运动到B点,重力做功分别为W1、W2,所用时间分别为t1、t2,则它们的大小关系为( )
如图所示,一物体从A点先后沿光滑路径Ⅰ、Ⅱ运动到B点,重力做功分别为W1、W2,所用时间分别为t1、t2,则它们的大小关系为( )
 如图所示,一物体从A点先后沿光滑路径Ⅰ、Ⅱ运动到B点,重力做功分别为W1、W2,所用时间分别为t1、t2,则它们的大小关系为( )
如图所示,一物体从A点先后沿光滑路径Ⅰ、Ⅱ运动到B点,重力做功分别为W1、W2,所用时间分别为t1、t2,则它们的大小关系为( )| A. | W1≠W2 | B. | W1=W2 | C. | t1=t2 | D. | t1≠t2 |
18. 质量为m的小物块在倾角为α的斜面上处于静止状态,如图所示.若斜面体和小物块一起以速度v沿水平方向向右做匀速直线运动,通过一段位移s.斜面体对物块的摩擦力和支持力的做功情况是( )
质量为m的小物块在倾角为α的斜面上处于静止状态,如图所示.若斜面体和小物块一起以速度v沿水平方向向右做匀速直线运动,通过一段位移s.斜面体对物块的摩擦力和支持力的做功情况是( )
 质量为m的小物块在倾角为α的斜面上处于静止状态,如图所示.若斜面体和小物块一起以速度v沿水平方向向右做匀速直线运动,通过一段位移s.斜面体对物块的摩擦力和支持力的做功情况是( )
质量为m的小物块在倾角为α的斜面上处于静止状态,如图所示.若斜面体和小物块一起以速度v沿水平方向向右做匀速直线运动,通过一段位移s.斜面体对物块的摩擦力和支持力的做功情况是( )| A. | 摩擦力做正功,支持力做正功 | B. | 摩擦力做正功,支持力做负功 | ||
| C. | 摩擦力做负功,支持力做正功 | D. | 摩擦力做负功,支持力做负功 |
